Difference between revisions of "ANOVA"
| Line 60: | Line 60: | ||
== Key Publications == | == Key Publications == | ||
| − | + | '''Theoretical''' | |
| + | Crawley, M. J. (2007). The R book. John Wiley & Sons. | ||
== References == | == References == | ||
Revision as of 06:34, 2 August 2022
Note: This entry introduces the Analysis of Variance. For more on Experiments, in which ANOVAs are typically conducted, please refer to the enries on Experiments, Experiments and Hypothesis Testing as well as Field experiments.
| Method categorization | ||
|---|---|---|
| Quantitative | Qualitative | |
| Inductive | Deductive | |
| Individual | System | Global |
| Past | Present | Future |
In short: The Analysis of Variance is a statistical method that allows to test differences of the mean values of groups within a sample.
Background
With a rise in knowledge during the Enlightenment, it became apparent that the controlled setting of a laboratory were not enough for experiments, as it became obvious that more knowledge was there to be discovered in the real world. First in astronomy, but then also in agriculture and other fields, the notion became apparent that our reproducible settings may sometimes be hard to achieve within real world settings. Observations can be unreliable, and errors in measurements in astronomy was a prevalent problem in the 18th and 19th century. Fisher equally recognised the mess - or variance - that nature forces onto a systematic experimenter (Rucci & Tweney 1980). The demand for more food due to the rise in population, and the availability of potent seed varieties and fertiliser - both made possible thanks to scientific experimentation - raised the question how to conduct experiments under field conditions.
Consequently, building on the previous development of the t-test, Fisher proposed the Analysis of Variance, abbreviated as ANOVA (Rucci & Tweney 1980). It allowed for the comparison of variables from experimental settings, comparing how a continuous variable fared under different experimental settings. Doing experiments in the laboratory reached its limits, as plant growth experiments were hard to conduct in the small confined spaces of a laboratory. It also became questionable whether the results were actually applicable in the real world. Hence experiments literally shifted into fields, with a dramatic effect on their design, conduct and outcome. While laboratory conditions aimed to minimise variance - ideally conducting experiments with a high confidence -, the new field experiments increased sample size to tame the variability - or messiness - of factors that could not be controlled, such as subtle changes in the soil or microclimate. Fisher and his ANOVA became the forefront of a new development of scientifically designed experiments, which allowed for a systematic testing of hypotheses under field conditions, taming variance through replicates. The power of repeated samples allowed to account for the variance under field conditions, and thus compare differences in mean values between different treatments. For instance, it became possible to compare different levels of fertiliser to optimise plant growth.
Establishing the field experiment became thus a step in the scientific development, but also in the industrial capabilities associated to it. Science contributed directly to the efficiency of production, for better or worse. Equally, the systematic experiments translated into other domains of science, such as psychology and medicine.
What the method does
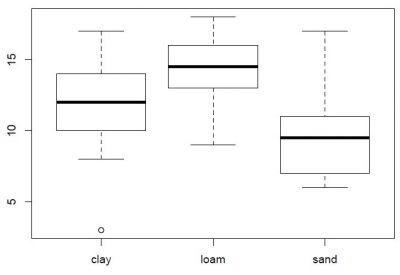
The ANOVA is a deductive statistical method that allows to compare how a continuous variable differs under different treatments in a designed experiment. It is one of the most important statistical models, and allows for an analysis of data gathered from designed experiments. In an ANOVA-designed experiment, several categories are thus compared in terms of their mean value regarding a continuous variable. A classical example would be how a certain type of barley grows on different soil types, with the three soil types loamy, sandy and clay (Crawley 2007, p. 449). If the majority of the data from one soil type differs from the majority of the data from the other soil type, then these two types differ, which can be tested by a t-test. The ANOVA is in principle comparable to the t-test, but extends it: it can compare more than two groups, hence allowing to compare data in more complex, designed experiments.
Single factor analysis that are also called 'one-way ANOVAs' investigate one factor variable, and all other variables are kept constant. Depending on the number of factor levels these demand a so called randomisation, which is necessary to compensate for instance for microclimatic differences under lab conditions.
Designs with multiple factors or 'two way ANOVAs' test for two or more factors, which then demands to test for interactions as well. This increases the necessary sample size on a multiplicatory scale, and the degrees of freedoms may dramatically increase depending on the number of factors levels and their interactions. An example of such an interaction effect might be an experiment where the effects of different watering levels and different amounts of fertiliser on plant growth are measured. While both increased water levels and higher amounts of fertiliser right increase plant growths slightly, the increase of of both factors jointly might lead to a dramatic increase of plant growth.
The data that is of relevance to ANOVAs can be ideally visualised in boxplots, which allows for an initial visualisation of the data distribution, since the classical ANOVA builds on the regression model, and thus demands data that is normally distributed. If one box within a boxplot is higher or lower than the median of another factor level, then this is a good rule of thumb whether there is a significant difference. When making such a graphically informed assumption, we have to be however really careful if the data is normally distributed, as skewed distributions might tinker with this rule of thumb. The overarching guideline for the ANOVA are thus the p-values, which give significance regarding the difference between the different factor levels.
In addition, the original ANOVA builds on balanced designs, which means that all categories are represented by an equal sample size. Extensions have been developed later on in this regard, with the type 3 ANOVA allowing for the testing of unbalanced designs, where sample sizes differ between different categories levels. The Analysis of Variance is implemented into all standard statistical software, such as R and SPSS. However, differences in the calculation may occur when it comes to the calculation of unbalanced designs.
Strengths & Challenges
The ANOVA can be a powerful tool to tame the variance in field experiments or more complex laboratory experiments, as it allows to account for variance in repeated experimental measures of experiments that are built around replicates. The ANOVA is thus the most robust method when it comes to the design of deductive experiments, yet with the availability of more and more data, also inductive data has increasingly been analysed by use of the ANOVA. This was certainly quite alien to the original idea of Fisher, who believed in clear robust designs and rigid testing of hypotheses. The reproducibility crisis has proven that there are limits to deductive approaches, or at least to the knowledge these experiments produce. The 20th century was certainly fuelled in its development by experimental designs that were at their heart analysed by the ANOVA. However, we have to acknowledge that there are limits to the knowledge that can be produced, and more complex analysis methods evolved with the wider availability of computers.
In addition, the ANOVA is equally limited as the regression, as both build on the normal distribution. Extensions of the ANOVA translated its analytical approach into the logic of generalised linear models, enabling the implementation of other distributions as well. What unites all different approaches is the demand that the ANOVA has in terms of data, and with increasing complexity, the demands increase when it comes to the sample sizes. Within experimental settings, this can be quite demanding, which is why the ANOVA only allows to test very constructed settings of the world. All categories that are implemented as predictors in an ANOVA design represent a constructed worldview, which can be very robust, but is always a compromise. The ANOVA thus tries to approximate causality by creating more rigid designs. However, we have to acknowledge that experimental designs are always compromises, and more knowledge may become available later. Within clinical trials - most of which have an ANOVA design at their heart - great care is taken into account in terms of robustness and documentation, and clinical trial stages are built on increasing sample sizes to minimise the harm on humans in these experiments.
Taken together, the ANOVA is one of the most relevant calculation tools to fuel the exponential growth that characterised the 20th century. Agricultural experiments and medical trials are widely built on the ANOVA, yet we also increasingly recognise the limitations of this statistical model. Around the millennium, new models emerged, such as mixed effect models. But at its core, the ANOVA is the basis of modern deductive statistical analysis.
Normativity
Designing an ANOVA-based design demands experience, and knowledge of the previous literature. The deductive approach of an ANOVA is thus typically embedded into an incremental development in the literature. ANOVA-based designs are therefore more often than not part of the continuous development in normal science. However, especially since the millennium, other more advanced approaches gained momentum, such as mixed effect models, information theoretical approaches, and structural equation models. The rigid root of the normal distribution and the basis of p-values is increasingly recognised as rigid if not outright flawed, and model reduction in more complex ANOVA designs is far from coherent between different branches of sciences. Some areas of science reject p-driven statistics altogether, while other branches of science are still publishing full models without any model reduction whatsoever. In addition, the ANOVA is today also often used to analyse inductive datasets, which is technically ok, but can infer several problems from a statistical standpoint, as well as based on a critical perspective rooted in a coherent theory of science.
Hence the ANOVA became a swiss army knive for group comparison for a continuous variable, and whenever different category levels need to be compared across a dependent variable, the ANOVA is being pursued. Whether there is an actual question of dependency is often ignored, let alone model assumptions and necessary preconditions. Science evolved, and with it, our questions became ever more complex, as are the problems that we face in the world, or that want to test. Complexity reigns, and simple designs are more often than not questioned. The ANOVA remains as one of the two fundamental models of deductive statistics, with regression being the other important line of thinking. As soon as rigid questions of dependence were conveniently ignored, statisticians - or the researchers that applied statistics - basically dug the grave for these rigid yet robust approaches. There are still many cases where the ANOVA represents the most parsimonious and even adequate model. However, as long as positivist scientists share a room with a view in their ivory tower and fail to clearly indicate the limitations of their ANOVA-based designs, they undermine their credibility, and with it the trust between science and society. The ANOVA is a testimony of how much statsicsi can serve society, for better or worse. The ANOVA may serve as a sound approximations of knowledge, yet at its worst it speaks of the arrogance of researchers who imply causality into mere patterns that can and will change once more knowledge becomes available.
Outlook
The Analysis of Variance was one of the most relevant contributions of statistics to the developments of the 20th century. By allowing for the systematic testing of hypotheses, not only did a whole line of thinking of the theory of science evolve, but whole disciplines were literally emerging. Lately, frequentist statistics was increasingly critizised for its reliance on p-values. Also, the reproducibility crisis highlights the limitations of ANOVA-based designs, which are often not reproducible. Psychological research faces this challenge for instance by pre-registering studies, indicating their statistical approach before approaching the data, and other branches of science are also attempting to do more justice to the limitations of the knowledge of experiments. In addition, new ways of experimentation of science evolve, introducing a systematic approach to case studies and solution oriented approaches. This may open a more systematic approach to inductive experiments, making documentation a key process in the creation of a canonised knowledge. Scientific experiments were at the forefront of developments that are seen more critically regarding their limitations. Taking more complexities into account, ANOVAs become a basis for more advanced statistics, and they can indeed serve as a robust basis if the limitations are clearly indicated, and the ANOVA designs add to parts of a larger picture of knowledge.
Key Publications
Theoretical Crawley, M. J. (2007). The R book. John Wiley & Sons.
References
Crawley, M. J. (2007). The R book. John Wiley & Sons. Rucci, A. J., & Tweney, R. D. (1980). Analysis of variance and the" second discipline" of scientific psychology: A historical account. Psychological Bulletin, 87(1), 166.
The author of this entry is Henrik von Wehrden.