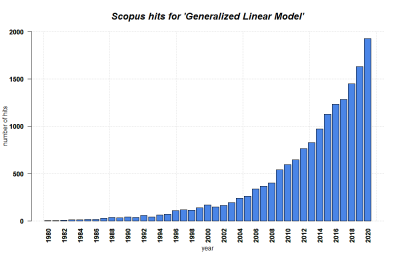
Generalized Linear Models
Quantitative - Qualitative
Deductive - Inductive
Individual - System - Global
Past - Present - Future
In short: Generalized Linear Models (GLM) are a family of models that are a generalization of ordinary linear regression, thereby allowing for different statistical distributions to be implemented.
Contents
Background
Being baffled by the restrictions of regressions that rely on the normal distribution, John Nelder and Robert Wedderburn developed Generalized Linear Models (GLMs) in the 1960s to encompass different statistical distributions. Just as Ronald Fisher, both worked at the Rothamsted Experimental Station, seemingly a breeding ground not only in agriculture, but also for statisticians willing to push the envelope of statistics. Nelder and Wadderburn extended Frequentist statistics beyond the normal distribution, thereby unlocking new spheres of knowledge that rely on distributions such as Poisson and Binomial. Nelder's and Wedderburn's work allowed for statistical analyses that were often much closer to real world datasets, and the array of distributions and the robustness and diversity of the approaches unlocked new worlds of data for statisticians. The insurance business, econometrics and ecology are only a few examples of disciplines that heavily rely on Generalized Linear Models. GLMs paved the road for even more complex models such as additive models and generalised mixed effect models. Today, Generalized Linear Models can be considered to be part of the standard repertoire of researchers with advanced knowledge in statistics.
What the method does
Generalized Linear Models are statistical analyses, yet the dependencies of these models often translate into specific sampling designs that make these statistical approaches already a part of an inherent and often deductive methodological approach. Such advanced designs are among the highest art of quantitative deductive research designs, yet Generalized Linear Models are used to initially check/inspect data within inductive analysis as well. Generalized Linear Models calculate dependent variables that can consist of count data, binary data, and are also able to calculate data that represents proportions. Mechanically speaking, Generalized Linear Models are able to calculate relations between continuous variables where the dependent variable deviates from the normal distribution. The calculation of GLMs is possible with many common statistical software solutions such as R and SPSS. Generalized Linear Models thus represent a powerful means of calculation that can be seen as a necessary part of the toolbox of an advanced statistician.
Strengths & Challenges
Generalized Linear Models allow powerful calculations in a messy and thus often not normally distributed world. Many datasets violate the assumption of the normal distribution, and this is where GLMs take over and clearly allow for an analysis of datasets that are often closer to dynamics found in the real world, particularly outside of designed studies. GLMs thus represented a breakthrough in the analysis of datasets that are skewed or imperfect, may it be because of the nature of the data itself, or because of imperfections and flaws in data sampling. In addition to this, GLMs allow to investigate different and more precise questions compared to analyses built on the normal distribution. For instance, methodological designs that investigate the survival in the insurance business, or the diversity of plant or animal species, are often building on GLMs. In comparison, simple regression approaches are often not only flawed within regression schemes, but outright wrong.
Since not all researchers build their analysis on a deep understanding of diverse statistical distributions, GLMs can also be seen as an educational means that enable a deeper understanding of the diversity of approaches, thus preventing wrong approaches from being utilised. A sound understanding of the most important GLM models can bridge to many other more advanced forms of statistical analysis, and safeguards analysts from compromises in statistical analysis that lead to ambiguous results at best.
Another advantage of GLMs is the diversity of evaluative criteria, which may help to understand specific problems within data distributions. For instance, presence/absence variables are often riddled by prevalence, which is the proportion between presence values and absence values. Binomial GLMs are superior in inspecting the effects of a skewed prevelance, allowing for a sound tracking of thresholds within models that can have direct consequences. Examples for this can be found in medicine regarding the identification of precise interventions to save a patients life, where based on a specific threshhold for instance in oxygen in the blood an artificial Oxygen sources needs to be provides to support the breathing of the patient.
Regarding count data, GLMs prove to be the better alternative to log-transformed regressions, not only in terms of robustness, but also regarding the statistical power of the analysis. Such models have become a staple in biodiversity research with the counting of species and the respective explanatory calculations. However, count models are not very abundantly used in econometrics. This is insofar surprising, as one would expect count models are most prevalent here, as much of economic dynamics is not only represented by count data, but much of economic data is actually count data, and follows a Poisson distribution.
Normativity
To date, there is a great diversity when it comes to the different ways how GLMs can be calculated, and more importantly, how their worth can be evaluated. In simple regression, the parameters that allow for an estimation of the quality of the model fit are rather clear. By comparison, GLMs depend on several parameters, not all of which are shared among the diverse statistical distributions that the calculations are built upon. More importantly, there is a great diversity between different disciplines regarding the norms of how these models are utilised. This makes comparisons between these models difficult, and often hampers a knowledge exchange between different knowledge domains. The diversity in calculations and evaluations is made worse by the associated diversity in terms and norms used in this context. GLMs are surely established within advanced statistics, yet more work will be necessary to approximate coherence until all disciplines are on the same page.
In addition, GLMs are often a part of very specific parts of science. Whether researchers implement GLMs or not is often depending on their education: it is not guaranteed that everybody is aware of their necessity and able to implement these advanced models. What makes this even more challenging is that within larger analyses, different parts of the dataset may be built upon different distributions, and it can be seen as inconvenient to report diverse GLMs that are based on different distributions, particularly because these are then utilising different evaluative criteria. The ideal world of a statistician may differ from the world of a researcher using these models, showcasing that GLMs cannot be taken for granted as of yet. Often, researchers still prioritise to follow disciplinary norms rather than go for comparability and coherence. Hence the main weakness of GLMs is a failure or flaw in the application of the model, which can be due to a lack of experience. This is especially concerning in GLMs, since such mistakes are more easily made than identified.
Since analyses using GLMs are often part of a larger analysis scheme, experience is typically more important than, for instance, with simple regressions. Particularly, questions of model reduction showcase how the pure reasoning of the frequentists and their probability values clashes with more advanced approaches such as Akaike Information Criterion (AIC) that builds upon a penalisation of complexity within models. Even within the same branch of science, the evaluation of p-values vs other approaches may differ, leading to clashes and continuous debates, for instance within the peer-review process of different approaches. Again, it remains to be seen how this development may end, but everything below a sound and overarching coherence will be a long-term loss, leading maybe not to useless results, but to at least incomparable ones. In times of Meta-Analysis, this is not a small problem.
Outlook
Integration of the diverse approaches and parameters utilised within GLMs will be an important stepping stone that should not be sacrificed just because even more specific analysis are already gaining dominance in many scientific disciplines. Solving the problems of evaluation and model selection as well as safeguarding the comparability of complexity reduction within GLMs will be the frontier on which these approaches will ultimately prove their worth. These approaches have been available for more than half of a century now, and during the last decades more and more people were enabled to make use of their statistical power. Establishing them fully as a part of the standard canon of statistics for researchers would allow for a more nuanced recognition of the world, yet in order to achieve this, a greater integration into students curricular programs will be a key goal.
Key Publications
The author of this entry is Henrik von Wehrden.