Difference between revisions of "Experiments and Hypothesis Testing"
| Line 86: | Line 86: | ||
[[File:Bildschirmfoto 2020-04-24 um 15.03.40.png|thumb|Uncertainty means that even the most careful and rigorous scientific investigation could not yield an exact measurement.]] | [[File:Bildschirmfoto 2020-04-24 um 15.03.40.png|thumb|Uncertainty means that even the most careful and rigorous scientific investigation could not yield an exact measurement.]] | ||
| − | In ancient Greece there were basically two types of knowledge. The first was the metaphysical which was quite diverse and some may say vague. The second was the physical or better mathematical which was quite precise | + | In ancient Greece there were basically two types of knowledge. The first was the metaphysical which was quite diverse and some may say vague. The second was the physical or better mathematical which was quite precise yet likewise diverse. With the rise of irrational numbers in medieval times, however, and the combination of the hypothesis testing thoughts in the enlightenment, uncertainty was born. By having larger samples i.e. through financial accounting and by making repeated measures in astronomy, biology and other sciences, a certain lack of precision became apparent in the empirical sciences. More importantly, the recognition of fluctuation, modifications, and other reasons for error became apparent. Soft sciences were on the rise, and this demanded a clearer recognition of errors within scientific analysis and reasoning. |
| − | While validity encompasses | + | While validity encompasses everything from theory building to a final confirmation, uncertainty is only preoccupied with the methodological dimension of hypothesis testing. Observations can be flawed, measurements can be wrong, an analysis can be biased and mis-selected, but at least this is it what uncertainty can tell us. [https://www.visionlearning.com/en/library/Process-of-Science/49/Uncertainty-Error-and-Confidence/157 '''Uncertainty] is hence a word for all the errors that can be done within a methodological application.''' Better yet, uncertainty can thus give us the difference between a perfect model and our empirical results. Uncertainty is important to recognise how good our hypothesis or model can be confirmed by empirical data, and all the measurements errors and missed selections in analysis associated to it. |
What makes uncertainty so practical is the fact that many statistical analysis have a measure to quantify uncertainty, and due to repeated sampling we can thus approximate the so-called "error" of our statistical test. The [https://www.youtube.com/watch?v=tFWsuO9f74o confidence interval] is a classic example of such a quantification of an error of a statistical result. Since it is closely associated with probability, the confidence interval can tell us the chance with which our results are reproducible. While this sounds like a small detail, it is of huge importance in modern statistics. Uncertainty allowed us to quantify whether a specific analysis can be reliably repeated and thus the result can have relevance under comparable conditions. | What makes uncertainty so practical is the fact that many statistical analysis have a measure to quantify uncertainty, and due to repeated sampling we can thus approximate the so-called "error" of our statistical test. The [https://www.youtube.com/watch?v=tFWsuO9f74o confidence interval] is a classic example of such a quantification of an error of a statistical result. Since it is closely associated with probability, the confidence interval can tell us the chance with which our results are reproducible. While this sounds like a small detail, it is of huge importance in modern statistics. Uncertainty allowed us to quantify whether a specific analysis can be reliably repeated and thus the result can have relevance under comparable conditions. | ||
Consider the example of medical treatment that has a high uncertainty identified with it. Would you undergo the procedure? No one in their right mind would trust treatment that has a high uncertainty. Hence uncertainty became the baseline of scientific outcome in quantitative science. It should be noted that this also opened the door to misuse and corruption. Many scientists measure their sceintific merit by their model with the lowest uncertainty, and quite some misuse has been done through the boundless search of tackling uncertainty. Yet we need to be aware that wrong understandings of statistics and severe cases of scientific misconduct are an exception and not the norm. If scientific results are published, we can question them, but we cannot question their sound and safe measures that have been established over the decades. Uncertainty can still be a guide helping us to identify the likelihood of our results matching a specific reality. | Consider the example of medical treatment that has a high uncertainty identified with it. Would you undergo the procedure? No one in their right mind would trust treatment that has a high uncertainty. Hence uncertainty became the baseline of scientific outcome in quantitative science. It should be noted that this also opened the door to misuse and corruption. Many scientists measure their sceintific merit by their model with the lowest uncertainty, and quite some misuse has been done through the boundless search of tackling uncertainty. Yet we need to be aware that wrong understandings of statistics and severe cases of scientific misconduct are an exception and not the norm. If scientific results are published, we can question them, but we cannot question their sound and safe measures that have been established over the decades. Uncertainty can still be a guide helping us to identify the likelihood of our results matching a specific reality. | ||
| − | |||
== The history of laboratory experiments == | == The history of laboratory experiments == | ||
Revision as of 14:35, 13 November 2023
Note: The German version of this entry can be found here: Experiments and Hypothesis Testing (German)
Note: This entry is a brief introduction to experiments. For more details, please refer to the entries on Experiments, Case studies and Natural experiments as well as Field experiments.
In short: This entry introduces you to the concept of hypotheses and how to test them systematically.
| Method categorization | ||
|---|---|---|
| Quantitative | Qualitative | |
| Inductive | Deductive | |
| Individual | System | Global |
| Past | Present | Future |
Hypothesis building
Life is full of hypotheses. We are all puzzled by an endless flow of questions. We constantly test our surrounding for potential what ifs, cluttering our mind, yet more often is our cluttered head unable to produce any generalizable knowledge. Still, our brain helps us filter our environment, also by constantly testing questions - or hypotheses - to enable us to better cope with the challenges we face. It is not really the big questions that keep us pre-occupied every day, but these small questions keep us going.
Did you ever pick the wrong food in a restaurant? Then your brain writes a little note to itself, and next time you pick something else. This enables us to find our niche in life. However, at some point, people started observing patterns in their environment and communicated these to other people. Collaboration and communication were our means to become communities and much later, societies. This dates back to before the dawn of humans and can be observed for other animals as well. Within our development, it became the backbone of our modern civilization – for better or worse - once we tested our questions systematically. James Lind, for example, conducted one of these first systematic approaches at sea and managed to find a cure for the disease scurvy, which caused many problems to sailors in the 18th century.
Hypothesis Testing
Specific questions rooted in an initial idea, a theory, were thus tested repeatedly. Or perhaps it is better to say these hypotheses were tested with replicates and the influences disturbing our observation were kept constant. This is called testing of hypothesis, the repeated systematic investigation of a preconceived theory, where during the testing ideally everything is kept constant except for what is being investigated. While some call this the "scientific method," Many researchers are not particularly fond of this label, as it implies that it is THE scientific method, which is certainly not true. Still, the systematic testing of the hypothesis and the knowledge process that resulted from it was certainly a scientific revolution (for more information, click here).
What is important regarding this knowledge is the notion that a confirmed hypothesis indicates that something is true, but other previously unknown factors may falsify it later. This is why hypothesis testing allows us to approximate knowledge, many would argue, with a certain confidence, but we will never truly know something. While this seems a bit confusing, a prominent example may help illustrate this. Before discovering Australia, all swans known in Europe were white. With the discovery of Australia, and to the surprise of Natural History researchers at the time, black swans were discovered. Hence before that, everybody would have hypothesized: all swans are white. Then Australia was discovered, and the world changed, or at least, the knowledge of Western cultures about swans.
At this point it is important to know that there are two types of hypotheses. Let us imagine that you assume, there are not only white swans in the world, but also black swans. The null hypothesis (H0) states that this is not the case - everything is as we assumed before you came around the corner with your crazy claim. Therefore, the null hypothesis would be: all swans are white. The alternative hypothesis (H1) now challenges this null hypothesis: there are also black swans. This is what you claimed in the first place. We do not assume however right away that whatever you came up with is true, so we make it the alternative hypothesis. The idea is now to determine whether there is enough evidence to support the alternative hypothesis. To do so, we test the likelihood of the H0 being true in order to decide whether to accept the H0, or if we reject it and rather accept the H1. Both go together - when we accept one of both hypotheses, we simultaneously reject the other hypothesis, and vice-versa. Caution: hypotheses can only be rejected, they cannot be verified based on data. When it is said that a hypothesis is 'accepted' or 'verified' or 'proven', this only means that the alternative cannot be supported, and we therefore stick to the more probable hypothesis.
Errors in Hypothesis Testing
In hypothesis testing, there are two different errors that can occur. The false positive ("Error Type I") and false negative ("Error Type II"). If a doctor diagnoses someone to be pregnant and the person is not, this is a typical false positive error. The doctor has claimed that the person is pregnant, which is not the case. The other way around, if the doctor diagnoses someone not to be pregnant, but in fact, that person is, this is a typical false negative error. Each and everyone may judge by themselves which kind of error is more hazardous. Nevertheless, both errors are to be avoided. During the Corona crisis, this became an important topic, as many of the tests were often wrong. If someone with Corona showed symptoms but tested negative, it was a false negative. This depends seemingly on the time of testing and the respective tests. Antibody tests are only relevant after someone had Corona, but sometimes even these may not find any antibodies. During an active case only a PCR can confirm an infection, but taking a sample is tricky, hence again there were some false negatives. False positives are however very rare, as the error rate of the test to this end is very low. Still, sometimes samples got messed up. Rarely, but it happened, creating a big stir in the media.
Knowledge may change over time
In modern science great care is taken to construct hypotheses that are systematically sound, meaning that black swans are not to be expected, but sometimes they cannot be prevented. An example is whether a medication is suitable for pregnant persons. For ethical reasons, this is hardly ever tested, which had severely negative impacts in the past. Hence, knowledge of how a specific medication affects pregnant persons is often based on experience, but not systematically investigated. Taken together, hypotheses became a staple of modern science, although they represent only one concept within the wide canon of scientific methods. The dependency on deductive approaches has in the past also posed problems, and may indirectly lead to building a wall between knowledge created by inductive vs. deductive approaches.
An example: Finding a vaccine for Covid-19
Many consider a vaccine to be the safest end of the pandemic. Only time will tell if this is actually true, yet research points in a clear direction. We thus have the hypothesis, but we have not tested the hypothesis yet, as it was not possible. More importantly, almost all vaccines currently run through clinical trials that test so many more hypotheses. Is the vaccine safe for people, are there no side effect, allergic reaction or other severe medical problems? Does the vaccine create an immune response? And does it affect different age groups or other groups differently? In order to safely test these strategies, clinical trials emerged over the last decades as the gold standard in modern day experiments. Many may criticize modern science, and question much of what science has done to contribute not only to positive development in our society. Nevertheless, many of us owe our lives to such clinical trails - the safe and sound testing of scientific hypotheses, under very reproducible conditions. Much of modern medicine, psychology, product testing and also agriculture owe their impact onto our societies to the experiment.
Key messages
• Hypothesis testing is the repeated systematic investigation of a preconceived idea through observation
• There is a differentiation between the null hypothesis (H0), which we try to reject, and alternative hypothesis (H1)
• There are two different errors that can occur, false positive ("Error Type I") and false negative ("Error Type II")
Validity
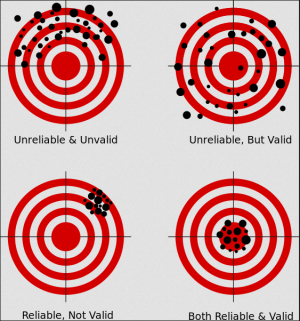
Validity is derived from the Latin word "validus" which translates as "strong". It is thus a central concept within hypothesis testing, as it qualifies to which extent a hypothesis is true. Its meaning should not be confused with reliability which indicates whether certain results are consistent, or in other words reproducible. Validity instead indicates the extent to which a hypothesis can be confirmed. As a consequence, it is central for the deductive approach in science; in other words: it should not be misused beyond that line of thinking. Validity is therefore strongly associated with reasoning, which is why it indicates the overall strength of the outcome of a statistical result.
We should however be aware that validity encompasses the whole process of the application of statistics. Validity spans from the postulation of the original hypothesis over the methodological design, the choice of analysis and finally the interpretation. Validity is hence not an all or nothing. Instead we need to learn the diverse approaches and flavours of validity, and only experience across diverse datasets and situations will allow us to judge whether a result is valid or not. This is one of the situations where statistics and philosophy are maybe the closest. In philosophy it is very hard to define reason, and much of Western philosophy has been indeed devoted to reason. While it is much easier to define unreasonable acts (and rationality is altogether a different issue), reason in itself is more complex, many would argue. Consequently, validity of the question whether the confirmation of a hypothesis is reasonable, is much harder to answer. Take your time to learn about validity, and take even more time to gain experience on wether a result is valid.
Reliability
Reliability is one of the key concepts of statistics. It is defined as the consistency of a specific measure. A reliable measure is hence producing comparable results under the same conditions. Reliability gives you an idea whether your analysis is accurate under the given conditions and also reproducible. We already learned that most, if not all, measures in statistics are constructed. Reliability is central since we can check whether our constructed measures bring us on the right track. In other words, reliability allows us to understand if our constructed measures are working.
The question of reproducibility which is associated to reliability is a central aspect of modern science. Reliability is hence the concept that contains at least several components.
1. The extent and complexity of the measure that we include in our analysis. While it cannot be generally assumed that extremely constructed measures such as GDP or IQ are less reliable than less constructed ones, we should still consider Occam's razor when thinking about the reliability of measures, i.e. keep your constructs short and simple.
2. Relevant for reliability is the question of our sample. If external conditions of the sample change then, due to new information, reliability might decrease. An easy example would again be swans. If we state that there are just white swans, this hypothesis is reliable as long as there are just white swans sampled. But when the external conditions change - for example when we discover black swans in Australia - the reliability of our first hypothesis decreases.
3. Furthermore, sampling can also be affected. If sampling is done by several observers then a reduction in reliability may be explained by the differences of the respective observers.
4. We have to recognise that different methodological approaches - or more specifically in our case, statistical tests - may consist of different measures of reliability. Hence the statistical model of our analysis might directly translate into different reliabilities. An easy example to explain this a bit better is the one sample test with a perfect coin. This test should work but it does not work anymore when the coin is biased. Then we have to consider a new method/model to explain this (namely the "two sample test"). The important thing to remember is: The choice of your method/model has an impact on your test results.
5. The last aspect of reliability is related to our theoretical foundation itself. If our underlying theory is revised or changed, then this might tinker with the overall reliability of our results. This is important to highlight, since we might have an overall better theoretical foundation within a given statistical analysis, however the statistical measure of reliability might be lower. This is a source of continuous confusion among apprentices in statistics.
The question how reliable statistical analysis or better the result of a scientific study is, is in my experience the source of endless debates. There is no measure of reliability that is accepted by everybody. Instead, statistics are still evolving, and measures of reliability change. While this seems confusing at first, we should differentiate between results that are extremely reliable and results that are lower in terms of reliability. Results from hard science such as physics often show a high reliability when it comes to statistical testing, while soft science such as psychology and economics can be found at the lower end of reliability. There is no normative judgement employed here, since modern medicine often produces results that are reliable, but only just so. Consider research in cancer. Most current breakthroughs change the lives of a few percentages of patients and there is hardly a breakthrough that can affect a larger proportion of patients. We thus have to accept reliability in statistics as a moving target, and it depends very much on the context whether a result is having a high or low reliability.
Uncertainty
In ancient Greece there were basically two types of knowledge. The first was the metaphysical which was quite diverse and some may say vague. The second was the physical or better mathematical which was quite precise yet likewise diverse. With the rise of irrational numbers in medieval times, however, and the combination of the hypothesis testing thoughts in the enlightenment, uncertainty was born. By having larger samples i.e. through financial accounting and by making repeated measures in astronomy, biology and other sciences, a certain lack of precision became apparent in the empirical sciences. More importantly, the recognition of fluctuation, modifications, and other reasons for error became apparent. Soft sciences were on the rise, and this demanded a clearer recognition of errors within scientific analysis and reasoning.
While validity encompasses everything from theory building to a final confirmation, uncertainty is only preoccupied with the methodological dimension of hypothesis testing. Observations can be flawed, measurements can be wrong, an analysis can be biased and mis-selected, but at least this is it what uncertainty can tell us. Uncertainty is hence a word for all the errors that can be done within a methodological application. Better yet, uncertainty can thus give us the difference between a perfect model and our empirical results. Uncertainty is important to recognise how good our hypothesis or model can be confirmed by empirical data, and all the measurements errors and missed selections in analysis associated to it.
What makes uncertainty so practical is the fact that many statistical analysis have a measure to quantify uncertainty, and due to repeated sampling we can thus approximate the so-called "error" of our statistical test. The confidence interval is a classic example of such a quantification of an error of a statistical result. Since it is closely associated with probability, the confidence interval can tell us the chance with which our results are reproducible. While this sounds like a small detail, it is of huge importance in modern statistics. Uncertainty allowed us to quantify whether a specific analysis can be reliably repeated and thus the result can have relevance under comparable conditions.
Consider the example of medical treatment that has a high uncertainty identified with it. Would you undergo the procedure? No one in their right mind would trust treatment that has a high uncertainty. Hence uncertainty became the baseline of scientific outcome in quantitative science. It should be noted that this also opened the door to misuse and corruption. Many scientists measure their sceintific merit by their model with the lowest uncertainty, and quite some misuse has been done through the boundless search of tackling uncertainty. Yet we need to be aware that wrong understandings of statistics and severe cases of scientific misconduct are an exception and not the norm. If scientific results are published, we can question them, but we cannot question their sound and safe measures that have been established over the decades. Uncertainty can still be a guide helping us to identify the likelihood of our results matching a specific reality.
The history of laboratory experiments
Experiments describe the systematic and reproducible design to test specific hypothesis.
Starting with Francis Bacon there was the theoretical foundation to shift previously widely un-systematic experiments into a more structured form. With the rise of disciplines in the enlightenment experiments thrived, also thanks to an increasing amount of resources available in Europe due to the Victorian age and other effects of colonialism. Deviating from more observational studies in physics, astronomy, biology and other fields, experiments opened the door to the wide testing of hypothesis. All the while Mill and others build on Bacon to derive the necessary basic debates about so called facts, building the theoretical basis to evaluate the merit of experiments. Hence these systematic experimental approaches aided many fields such as botany, chemistry, zoology, physics and much more, but what was even more important, these fields created a body of knowledge that kickstarted many fields of research, and even solidified others. The value of systematic experiments, and consequently systematic knowledge created a direct link to practical application of that knowledge. The scientific method -called with the ignorant recognition of no other methods beside systematic experimental hypothesis testing as well as standardisation in engineering- hence became the motor of both the late enlightenment as well as the industrialisation, proving a crucial link between basically enlightenment and modernity.
Due to the demand of systematic knowledge some disciplines ripened, meaning that own departments were established, including the necessary laboratory spaces to conduct experiments. The main focus to this end was to conduct experiments that were as reproducible as possible, meaning ideally with a 100 % confidence. Laboratory conditions thus aimed at creating constant conditions and manipulating ideally only one or few parameters, which were then manipulated and therefore tested systematically. Necessary repetitions were conducted as well, but of less importance at that point. Much of the early experiments were hence experiments that were rather simple but produced knowledge that was more generalisable. There was also a general tendency of experiments either working or not, which is up until today a source of great confusion, as an trial and error approach -despite being a valid approach- is often confused with a general mode of “experimentation”. In this sense, many people consider preparing a bike without any knowledge about bikes whatsoever as a mode of “experimentation”. We therefore highlight that experiments are systematic. The next big step was the provision of certainty and ways to calculate uncertainty, which came with the rise of probability statistics.
First in astronomy, but then also in agriculture and other fields the notion became apparent that our reproducible settings may sometimes be hard to achieve. Error of measurements in astronomy was a prevalent problem of optics and other apparatus in the 18th and 19th century, and Fisher equally recognised the mess -or variance- that nature forces onto a systematic experimenter. The laboratory experiment was hence an important step towards a systematic investigation of specific hypothesis, underpinned by newly established statistical approaches.
For more on the laboratory experiment, please refer to the entry on Experiments.
The history of the field experiment
With a rise in knowledge, it became apparent that the controlled setting of a laboratory was not enough. First in astronomy, but then also in agriculture and other fields the notion became apparent that our reproducible settings may sometimes be hard to achieve. Observations can be unreliable, and error of measurements in astronomy was a prevalent problem in the 18th and 19th century. Fisher equally recognised the mess - or variance - that nature forces onto a systematic experimenter. The demand for more food due to the rise in population, and the availability of potent seed varieties and fertiliser - both made possible thanks to scientific experimentation - raised the question how to conduct experiments under field conditions. Making experiments in the laboratory reached its outer borders, as plant growth experiments were hard to conduct in the small confined spaces of a laboratory, and it was questioned whether the results were actually applicable in the real world. Hence experiments literally shifted into fields, with a dramatic effect on their design, conduct and outcome. While laboratory conditions aimed to minimise variance - ideally conducting experiments with a high confidence -, the new field experiments increased sample size to tame the variability - or messiness - of factors that could not be controlled, such as subtle changes in the soil or microclimate. Establishing the field experiment became thus a step in the scientific development, but also in the industrial development. Science contributed directly to the efficiency of production, for better or worse.
For more details on field experiments, please refer to the entry on Field experiments.
Enter the Natural experiments
Out of a diverse rooting in discussions about complexity, system thinking and the need to understand specific contexts more deeply, the classic experimental setting did at some point become more and more challenged. What emerged out of the development of field experiments was an almost exact opposite trend considering the reduction of complexity. What do we learn from singular cases? How do we deal with cases that are of pronounced importance, yet cannot be replicated? And what can be inferred from the design of such case studies? A famous example from ethnographic studies is the Easter Island. Why did the people there channel much of their resources into building gigantic statues, thereby bringing their society to the brink of collapse? While this is a surely intriguing question, there are no replicates of the Easter Islands. This is at a first glance a very specific and singular problem, yet it is often considered to be an important example on how unsustainable behaviour led to a collapse of a while civilisation. Such settings are referred to as Natural Experiments. From a certain perspective, our whole planet is a Natural Experiment, and it is also from a statistical perspective a problem that we do not have any replicates, besides other ramifications and unclarity that derives such single case studies, which are however often increasingly relevant on a smaller scale as well. With a rise in qualitative methods both in diversity and abundance, and an urge for understanding even complex systems and cases, there is clearly a demand for the integration of knowledge from Natural Experiments. From a statistical point of view, such cases are difficult and challenging due to a lack of being reproducible, yet the knowledge can still be relevant, plausible and valid. To this end, the concept of the niche in order to illustrate and conceptualise how single cases can still contribute to the production and canon of knowledge.
For example the financial crisis from 2007, where many patterns where comparable to previous crisis, but other factors were different. Hence this crisis is comparable to many previous factors and patterns regarding some layers of information, but also novel and not transferable regarding other dynamics. We did however understand based on the single case of this financial crisis that certain constructs in our financial systems are corrupt if not broken. The contribution to develop the financial world further is hence undeniable, even so far that many people agree that the changes that were being made are certainly not enough.
Another prominent example of a single case or phenomena is the Covid pandemic that emerges further. While much was learned from previous pandemics, this pandemic is different, evolves different, and creates different ramifications. The impact of our societies and the opportunity to learn from this pandemic is however undeniable. While classical experiments evolve knowledge like pawns in a chess game, moving forward step by step, a crisis such as the Covid pandemic is more like the horse in a chess game, jumping over larger gaps, being less predictable, and certainly harder to master. The evolution of knowledge in an interconnected world often demands a rather singular approach as a starting point. This is especially important in normative sciences, where for instance in conservation biology many researchers approach solutions through singular case studies. Hence the solution orientated agenda of sustainability science emerged to take this into account, and further.
To this end, real world experiments are the latest development in the diversification of the arena of experiments. These types of experiments are currently widely explored in the literature, yet there is no coherent understanding of what real-world experiments are to date in the available literature, yet approaches are emerging. These experiments can however be seen as a continuation of the trend of natural experiments, where a solution orientated agenda tries to generate one or several interventions, the effects of which are tested often within singular cases, but the evaluation criteria are clear before the study was conducted. Most studies to date have defined this with vigour; nevertheless, the development of real-world experiments is only starting to emerge.
For more details on natural experiments, please refer to the entry on Case studies and Natural experiments.
Experiments up until today
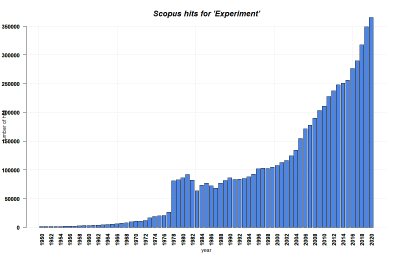
Diverse methodological approaches are thus integrated under the umbrella of the term 'experiment'. While simple manipulations such as medical procedures were already known as experiments during the enlightenment, the term 'experiment' gained in importance during the 20th century. Botanical experiments had been conducted long before, but it was the agricultural sciences that evolved the necessary methodological designs together with the suitable statistical analyses, creating a statistical revolution that created ripples in numerous scientific fields. The Analysis of Variance (ANOVA) become the most important statistical approach to this end, allowing for the systematic design of experimental settings, both in the laboratory and in agricultural fields.
While psychology, medicine, agricultural science, biology and later ecology thus thrived in their application of experimental designs and studies, there was also an increasing recognition of information that was creating biases or otherwise falsely skewed the results. The ANOVA hence became amended by additional modifications, ultimately leading to more advanced statistics that were able to focus on diverse statistical effects, and reduce the influence of skews rooted, for instance, in sampling bias, statistical bias or other flaws. Hence, Mixed-Effect Models became an advanced next step in the history of statistical models, leading to more complex statistical designs and experiments, taking more and more information into account. In addition, meta-analytical approaches led to the combination and summarising of several case studies into a systematic overview. This was the dawn of a more integrational understanding of different studies that were combined into a Meta-Analysis, taking different contexts of the numerous studies into account as well. In addition, research also focused more and more onto a deeper understanding of individual case studies, with a stronger emphasis on the specific context of the respective case. Such singular cases have been of value in medical research for decades now, where new challenges or solutions are frequently published despite the obvious lack of a wider contribution. Such medical case studies report novel findings, emerging problems or other so far unknown case dynamics, and often serve as a starting point for further research. Out of such diverse origins such as system thinking, Urban Research, Ethnography and other fields in research, real world experiments emerged, which take place in everyday social or cultural settings. The rigid designs of laboratory or field experiments is traded off for a deeper understanding of the specific context and case. While real world experiments emerged some decades ago already, they are only starting to gain wider recognition. All the while, the reproducibility crisis challenges the classical laboratory and field experiments, as a wider recognition that many results - for instance from psychological studies - cannot be reproduced. All this indicates that while much of our scientific knowledge is derived from experiments, much remains to be known, also about the conduct of experiments themselves.
The author of this entry is Henrik von Wehrden.