Revision as of 08:15, 23 March 2021

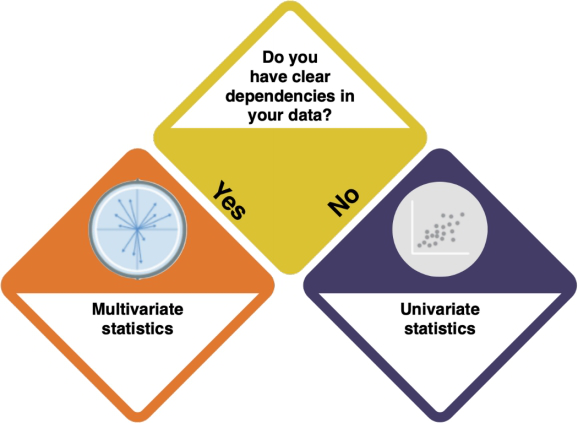
Start here with your data! This is your first question.

How do I know?

Inspect your data with str or summary. Are there several variables?
What does the data show? Does the underlying logic of the data suggest dependencies between the variables?

Example: Inspecting the swiss dataset

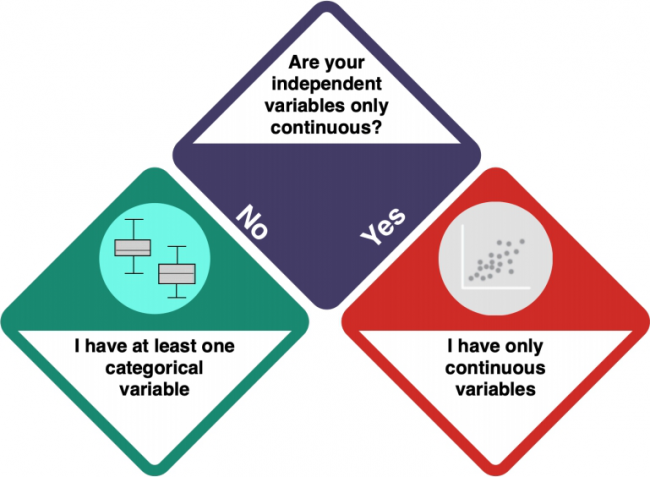
Univariate statistics

How do I know?

Check the entry on Data formats to understand the difference between categorical and numeric variables.
Investigate your data using str or summary. integer and numeric data is not categorical, while factorial and character data is.

Categorical variables

How do I know?

Investigate your data using str or summary. integer and numeric data is not categorical, while factorial and character data is.

LINK LEFT TO CHI SQUARE TEST R EXAMPLE

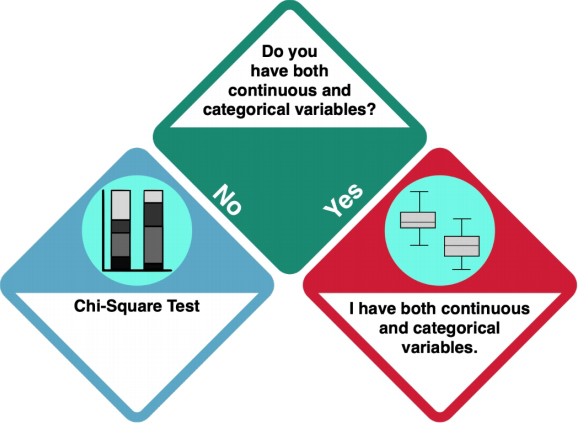
Categorical and continuous data

Statistics flowchart - Categorical factor levels.png

How do I know?

R commands: quantile(), str, summary
Investigate your categorical dependent variables using...
ADD MORE

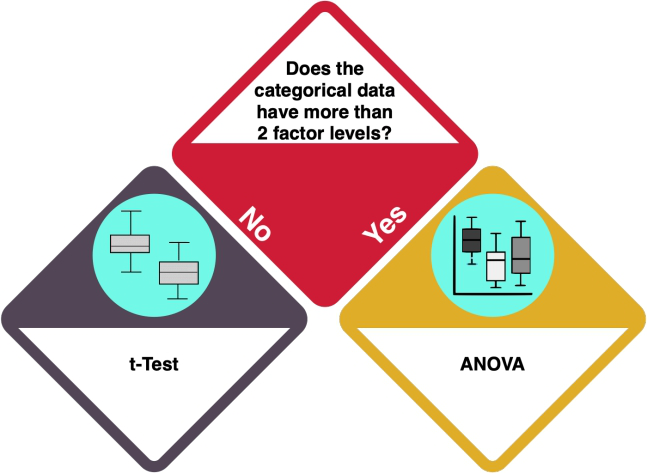
One or two factor levels

More than two factor levels

t-test

R commands: t.test, t_test Relevant figures:

No, my categorical dependent variables more than 2 factor levels!

Analysis of Variance

R commands: aov, Anova, ezAnova, var.test(), lm
Relevant figures: boxplot()

Is your dependent variable normally distributed?

R commands: ks.test, shapiro.test, hist

Yes, my dependent variable is normally distributed!
No, my dependent variable is binomial distributed!
No, my dependent variable is Poisson distributed!

Yes, my dependent variable is normally distributed!

Gaussian Anova

R commands: aov, lm
Relevant figures: boxplot

No, my dependent variable is not normally distributed!

Is your dependent variable binomial or Poisson

No, my dependent variable is Poisson distributed!

Dependent variable is count data

R commands: glm,
Relevant figures: plot

No, my dependent variable is binomial distributed!

Dependent variable is 0/1 or proportions

R commands:
Relevant figures:

Type III Anova

R commands: Anova(car)
Relevant figures: boxplot

Dependent variable not normally distributed

Dependent variable is count data

R commands: glm
Relevant figures: plot

Dependent variable is 0/1 or proportions

R commands: glm
Relevant figures:

Are there random factor variables?

Random factors

R commands: glmer, glmmPQL
Relevant figures:

Continuous variables

Non dependent relations?

Correlations

Clear dependent relations

Regression models

Dependent variable normally distributed

Linear Regression

Dependent variable not normally distributed

Generalised linear model

Dependent variable is count data

Dependent variable is 0/1 or proportions

R commands:
Relevant figures:

Yes, I have several continuous variables without clear dependencies!

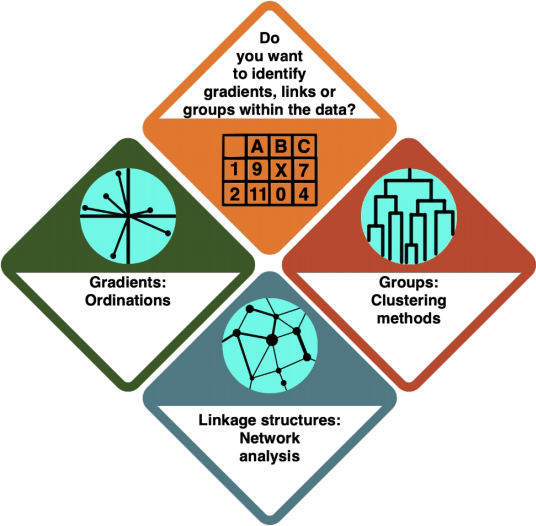
Multivariate statistics

Statistics Flowchart - Clustering, Networks, Ordination.png

How do I know?

In an Ordination, you arrange your data alongside underlying gradients in the variables to see which variables most strongly define the data points. Check the entry on Ordinations (to be added) to learn more.
In a Cluster Analysis, you group your data points according to how similar they are, resulting in a tree structure. Check the entry on Clustering Methods to learn more.
In a Network Analysis, you arrange your data in a network structure to understand their connections and the distance between individual data points. Check the entry on Social Network Analysis to learn more.

Data is classified into groups

R commands:
Relevant figures:

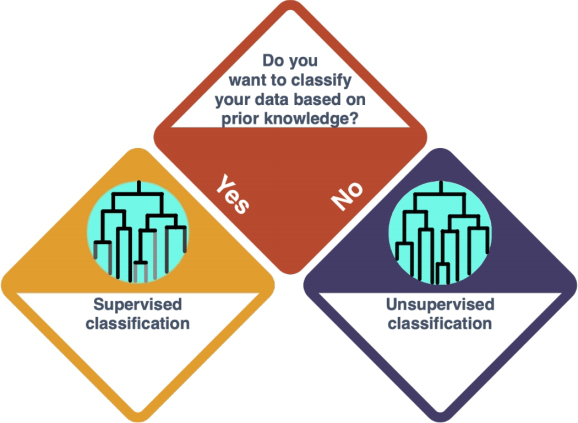
Cluster analysis

DIFFERENCE BETWEEN SUPERVISED AND UNSUPERVISED?? DISTINCTION NOT MADE IN THE CLUSTERING ENTRY

How do I know?

TAKE OUT LINK TO CLUSTERING METHODS ENTRY???

Supervised classification

R commands:
Relevant figures:

Unsupervised classification

R commands:
Relevant figures:

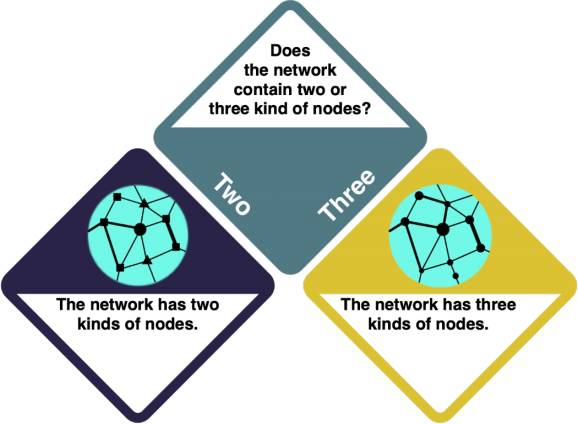
Network analysis

How do I know?

Check your data using the R code ADD CODE

ADD MORE BELOW

Bipartite

If your data has two different kinds of nodes, your network is called a "bipartite" network.

R commands:

is_bipartite(graph)
make_bipartite_graph(types, edges, directed = FALSE)

Tripartite

R commands:
Relevant figures:

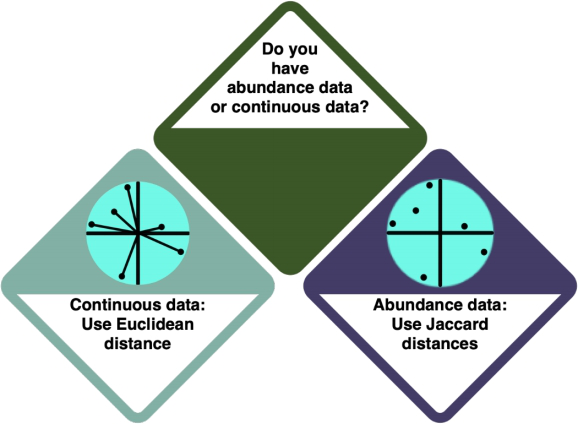
Ordinations

How do I know?

Check the entry on Data formats to learn more about the different data formats.
Investigate your data using str or summary. Abundance data is marked as FORMATNAME, and continuous data is marked as FORMATNAME.

MAKE THE STUFF BELOW CLEARER

Linear-based ordinations

Linear-based ordinations are... It uses Euclidean distances, which is... R commands:
Relevant figures:

Correspondance analysis

A correspondence analysis is... It uses Jaccard distances, which is... R commands:
Relevant figures:

More than 2 categorical variables

Is your dependent variable normally distributed?
Is your dependent variable not normally distributed?

My data consists only of categorical variables

Does your independent variable contain only 1 or 2 groups?
Does your independent variable contain more than 2 groups?

Does your independent variable contain more than 2 groups?

Is your dependent variable normally distributed?
Is your dependent variable not normally distributed?

Does your independent variable contain more only 1 or 2 groups?

My data consists only of categorical variables

Multivariate statistics

Resterampe

[[At least one continuous and one categorical variable| More than 2 groups Analysis of Variance
Dependent variable normally distributed
INSERT TYPE II
INSERT RANDOM FACTOR
INSERT LMM

Dependent variable not normally distributed

Type III Anova

Dependent variable is count data

Dependent variable is 0/1 or proportions

Random factors

@@ Line 3: / Line 3: @@
 <imagemap>Image:Statistics Flowchart - First Step.png|center|650px
 poly 328 376 12 696 332 1008 640 688 [[An_initial_path_towards_statistical_analysis#Multivariate_statistics|Multivariate Statistics]]
-poly 1068 436 744 752 1060 1080 1380 752 [[An_initial_path_towards_statistical_analysis#Univariate_statistics|Univariate Statistics]]
+poly 1064 372 732 700 1060 1008 1372 700 [[An_initial_path_towards_statistical_analysis#Univariate_statistics|Univariate Statistics]]
 </imagemap>
@@ Line 17: / Line 17: @@
 <imagemap>Image:Statistics Flowchart - Univariate Statistics.png|650px|center|
 poly 328 376 12 696 332 1008 640 688 [[An_initial_path_towards_statistical_analysis#Categorical_variables|Not only continuous variables]]
-poly 1056 368 732 696 1064 1000 1372 696 [[An_initial_path_towards_statistical_analysis#Continuous_variables|Only continuous variables]]
+poly 1064 372 732 700 1060 1008 1372 700 [[An_initial_path_towards_statistical_analysis#Continuous_variables|Only continuous variables]]
 </imagemap>
 '''How do I know?'''
@@ Line 27: / Line 27: @@
 <imagemap>Image:Statistics Flowchart - Data Formats.png|650px|center|
 poly 328 376 12 696 332 1008 640 688 [[Chi Square Test]]
-poly 1064 372 732 700 1060 1008 1372 684 [[An_initial_path_towards_statistical_analysis#Categorical_and_continuous_data|Categorical and continuous data]]
+poly 1064 372 732 700 1060 1008 1372 700 [[An_initial_path_towards_statistical_analysis#Categorical_and_continuous_data|Categorical and continuous data]]
 </imagemap>
@@ Line 39: / Line 39: @@
 <imagemap>Image:Statistics flowchart - Categorical factor levels.png|650px|center|
 poly 328 376 12 696 332 1008 640 688 [[An_initial_path_towards_statistical_analysis#One_or_two_factor_levels|One or two factor levels]]
-poly 1064 372 736 696 1076 996 1376 696 [[An_initial_path_towards_statistical_analysis#More_than_two_factor_levels|More than two factor levels]]
+poly 1064 372 732 700 1060 1008 1372 700 [[An_initial_path_towards_statistical_analysis#More_than_two_factor_levels|More than two factor levels]]
 </imagemap>
@@ Line 142: / Line 142: @@
 <imagemap>Image:Statistics Flowchart - Clustering, Networks, Ordination.png|center|650px|
 poly 328 368 12 692 332 1008 652 684 640 668 [[An_initial_path_towards_statistical_analysis#Ordinations|]]
-poly 1068 364 744 680 1064 1012 1376 688 1368 676 [[An_initial_path_towards_statistical_analysis#Cluster_analysis|]]
+poly 1064 372 732 700 1060 1008 1372 700 [[An_initial_path_towards_statistical_analysis#Cluster_analysis|]]
 poly 700 716 372 1044 700 1348 1012 1044 [[An_initial_path_towards_statistical_analysis#Network_analysis|]]
 </imagemap>
@@ Line 180: / Line 180: @@
 <imagemap>Image:Statistics Flowchart - Network Analysis.png|center|650px|
 poly 336 364 4 684 340 1000 644 692 632 676 [[Bipartite|Big problems for later|]]
-poly 1064 372 732 696 1060 1004 1372 688 [[Tripartite|Big problems for later]]
+poly 1064 372 732 700 1060 1008 1372 700 [[Tripartite|Big problems for later]]
 </imagemap>
@@ Line 201: / Line 201: @@
 <imagemap>Image:Statistics Flowchart - Ordination.png|650px|center|
 poly 332 372 8 692 328 1008 644 688 [[Big problems for later|Euclidean distances]]
-poly 1064 368 748 684 1060 996 1372 692 1372 692 [[Big problems for later|Jaccard distances]]
+poly 1064 372 732 700 1060 1008 1372 700 [[Big problems for later|Jaccard distances]]
 </imagemap>
 '''How do I know?'''

Difference between revisions of "An initial path towards statistical analysis"

Revision as of 08:15, 23 March 2021

Contents

Univariate statistics

Categorical variables

Categorical and continuous data

One or two factor levels

More than two factor levels

t-test

Analysis of Variance

Gaussian Anova

Dependent variable is count data

Dependent variable is 0/1 or proportions

Type III Anova

Dependent variable is count data

Dependent variable is 0/1 or proportions

Random factors

Continuous variables

Correlations

Regression models

Linear Regression

Generalised linear model

Dependent variable is count data

Dependent variable is 0/1 or proportions

Multivariate statistics

Data is classified into groups

Cluster analysis

Supervised classification

Unsupervised classification

Network analysis

Bipartite

Tripartite

Ordinations

Linear-based ordinations

Correspondance analysis