Difference between revisions of "Data formats (German)"
| (25 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
'''Note:''' This is the German version of this entry. The original, English version can be found here: [[Data formats]]. This entry was translated using DeepL and only adapted slightly. Any etymological discussions should be based on the English text. | '''Note:''' This is the German version of this entry. The original, English version can be found here: [[Data formats]]. This entry was translated using DeepL and only adapted slightly. Any etymological discussions should be based on the English text. | ||
| + | |||
| + | '''Kurz und knapp:''' Dieser Eintrag stellt unterschiedliche Datenformate vor. | ||
== Datenformate in der Statistik == | == Datenformate in der Statistik == | ||
| − | Das Format Ihrer Daten beeinflusst alles Andere, was Sie im weiteren Verlauf tun. Um ein Sprichwort zu paraphrasieren: Die Daten haben ein Format, und das Format sind die Daten. Deshalb ist es wichtig zu wissen, welche [https://www.youtube.com/watch?v=hZxnzfnt5v8 verschiedenen Datenformate] es gibt, und wie diese von Vorteil sein können, und wo Sie auf | + | Das Format Ihrer Daten beeinflusst alles Andere, was Sie im weiteren Verlauf Ihrer Arbeit tun. Um ein Sprichwort zu paraphrasieren: Die Daten haben ein Format, und das Format sind die Daten. Deshalb ist es wichtig zu wissen, welche [https://www.youtube.com/watch?v=hZxnzfnt5v8 verschiedenen Datenformate] es gibt, und wie diese von Vorteil sein können, und wo Sie auf Probleme stoßen können. Weitere Informationen zu verschiedenen Messmethoden finden Sie im Eintrag [[To Rule And To Measure (German)]]. |
| + | |||
| + | Der wichtigste Unterschied besteht zwischen quantitativen Daten und qualitativen Daten. Quantitative Daten können aus kontinuierlichen Daten, Intervalldaten und diskreten Daten bestehen, während qualitative Daten faktoriell - d. h. in wirklich verschiedenen Kategorien -, nominal oder ordinal sein können, wobei die beiden letzteren eine Verbindung zu quantitativen Daten herstellen. Die Nomenklatur für Datenformate ist jedoch in den verschiedenen Wissenschaftsbereichen sehr unterschiedlich, und um ehrlich zu sein, ein einziges Durcheinander. Wir versuchen hier, konsistent zu sein, aber seien Sie sich bitte bewusst, dass diese Bezeichnungen in der Wissenschaft nicht einheitlich sind. | ||
| + | |||
====Ein Beispiel für verschiedene Datenformate==== | ====Ein Beispiel für verschiedene Datenformate==== | ||
[[File:DataFormatsDiet.png|thumb|right|Ein Ernährungs-Tagebuch ist nur eines von vielen Beispielen, wie Sie verschiedene Datenformate angehen können]] | [[File:DataFormatsDiet.png|thumb|right|Ein Ernährungs-Tagebuch ist nur eines von vielen Beispielen, wie Sie verschiedene Datenformate angehen können]] | ||
| − | Stellen Sie sich vor, Sie wollen Ihre Ernährung tracken. Viele Menschen tun dies heute, es gibt überall | + | Stellen Sie sich vor, Sie wollen Ihre Ernährung tracken. Viele Menschen tun dies heute, es gibt überall Ernährungsbücher und -ratgeber, viele Informationen sind verfügbar geworden. Nun möchten Sie damit beginnen und sich mit dem, was Sie essen, besser vertraut machen. Wie würden Sie anfangen? Mit dem Zählen von Kalorien? Unterscheiden Sie zwischen Kohlenhydraten, Fett und Gemüse? Vielleicht zählen Sie einfach jedes Mal, wenn Sie eine Pizza gegessen haben? Oder Eiscreme? Oder "zu viel"? Es gibt viele Möglichkeiten, Ihre Ernährung zu messen. Und diese Messungen können in verschiedenen Datenformaten erfolgen. |
| + | |||
| + | Die meisten Datenformate können in andere Datenformate umgewandelt werden, was für viele Menschen oft verwirrend ist. Zum Beispiel können nominale Daten wiederholt gezählt werden, z. B. die verschiedenen Tassen Kaffee, die Sie jeden Tag trinken, wie ein Flat White und zwei Espressi. Die Anzahl der Tassen würde sich dann aufaddieren, was diskrete Daten darstellen würde. Ein anderes Beispiel wären die Körpergrößen von Menschen, die als kontinuierliche Daten in Metern dargestellt werden könnte. Dieses kann zwar in Zahlen dargestellt werden, aber auch in Kategorien, wie "klein" und "groß". | ||
| + | |||
| + | |||
| + | === Quantitative Daten === | ||
| + | '''Quantitative (numerische) Daten sind Daten, die in Zahlen ausgedrückt werden, mit denen sich rechnen lässt.''' Es gibt drei Arten numerischer Daten: Kontinuierliche und diskrete Daten, sowie Intervalldaten. | ||
====Kontinuierliche Daten==== | ====Kontinuierliche Daten==== | ||
| − | + | '''Kontinuierliche Daten sind numerische Daten die nicht gezählt werden können, weil sie auf einer endlichen oder unendlichen Skala existieren'''. Wir alle sind mit kontinuierlichen Zahlen vertraut. Ein Großteil unserer Gesellschaft wird von diesen Zahlen beherrscht, und daher wird ein Großteil der in der Statistik analysierten Daten durch kontinuierliche Zahlen dargestellt. Da ein Großteil der modernen Messungen innerhalb eines vorgegebenen Systems automatisiert ist, müssen wir uns oft nicht allzu viele Gedanken darüber machen, wie die Daten aussehen. Nehmen Sie zum Beispiel Gewicht oder Größe. Innerhalb von Mitteleuropa wird dies eindeutig in Gramm oder Kilogramm bzw. in Zentimetern oder Metern gemessen. Wenn Sie jedoch in die USA ziehen, wird es eine ganz andere Geschichte, wegen des [https://www.factmonster.com/math-science/weights-measures/metric-weights-and-measures metrischen Systems], oder eher dessen mangelnder Nutzung. Plötzlich sind Sie einige Fuß groß und wiegen vielleicht einige "stones". Es gibt viele [https://www.factmonster.com/math-science/weights-measures/the-international-system-metric verschiedene Messsysteme], und man muss sich bewusst sein, wie diese genutzt werden. Diese Systeme sind also Konstrukte, und diese Konstrukte bauen auf kontinuierlichen Zahlen auf. Dies zeigt, dass kontinuierliche Zahlen weit verbreitet sind, um Daten auszudrücken, aber wir müssen uns bewusst sein, dass es sich dabei immer noch um normative Informationen handelt. | |
| − | Wir alle sind mit kontinuierlichen Zahlen vertraut. Ein Großteil unserer Gesellschaft wird von diesen Zahlen beherrscht, und daher wird ein Großteil der in der Statistik analysierten Daten durch kontinuierliche Zahlen dargestellt. Da ein Großteil der modernen Messungen innerhalb eines vorgegebenen Systems automatisiert ist, müssen wir uns oft nicht allzu viele Gedanken darüber machen, wie die Daten aussehen. Nehmen Sie zum Beispiel Gewicht oder Größe. Innerhalb von | + | |
| + | Kontinuierliche Daten haben eine echte Null. Eine echte Null ist definiert als völlige Abwesenheit von etwas, das in Zahlen dargestellt werden kann. Obwohl ein Gewicht von 0 kg oder eine Länge von 0 m abstrakt sind, stellen die Werte die Abwesenheit von Gewicht bzw. Länge dar. | ||
| − | + | '''Beispiele für kontinuierliche Daten:'''<br/> | |
- die Zahl Pi: 3,14159265359... | - die Zahl Pi: 3,14159265359... | ||
<br> | <br> | ||
| Line 18: | Line 30: | ||
<br> | <br> | ||
- die Höhe des Empire State Buildings: 443,2m | - die Höhe des Empire State Buildings: 443,2m | ||
| − | |||
| − | |||
| − | ==== | + | ==== Diskrete Daten ==== |
| − | + | '''Diskrete Daten sind numerische Daten, die gezählt werden können, da sie nur als natürliche Zahlen (1, 2, 3, 4...) vorliegen'''. Beispiele hierfür sind Schüler*innen in einer Klasse, oder das eigene Alter. Hier ergibt es keinen Sinn, mit kontinuierlichen Daten zu arbeiten. Natürlich kann man auch an einen halbierten Apfel denken, aber wenn wir Äpfel, Vögel oder Studierende zählen, betrachten wir sie normalerweise als vollständige Einheiten und halten uns an natürliche Zahlen. Diskrete Daten werden oft auch als "Häufigkeits-" oder "Zähldaten" bezeichnet, und in der Sprache R werden sie als "integer" (Ganzzahlen) bezeichnet. | |
| − | [[File: | + | |
| − | Erinnern Sie sich an Ihre Schulnoten? Eine "1" ist die beste Note im deutschen Notensystem, aber ist sie doppelt so gut wie eine "2"? Wohl kaum. Solche Noten sind [http://intellspot.com/nominal-vs-ordinal-data/ ordinale Zahlen]. Es handelt sich dabei um ein System von Zahlen, die in gewisser Weise geordnet sind, aber die Zahlen an sich spiegeln nicht unbedingt ein numerisches System wider. Mit anderen Worten: Sie sind höchst normativ und umstritten. Eine "2" mag für die einen eine gute Note sein, für die anderen eine Katastrophe. Ordinale Formate sind oft klar definierte Skalen, die es Menschen ermöglichen, bestimmte Informationen zu benoten, zu bewerten oder in eine Rangfolge zu bringen. Eines der bekanntesten Beispiele ist die [ | + | Diskrete Daten haben auch eine echte Null. Nehmen wir noch einmal die Anzahl der Studierenden in einer Statistikvorlesung. Auch wenn die Vorlesung gut ist, zum Beispiel weil sie Lieder aus der Sesamstraße enthält, kann es sein, dass keine Studierenden in der Vorlesung sind. 0 Studierende in einer Vorlesung - da haben Sie Ihre echte Null. |
| + | |||
| + | ====Intervalldaten==== | ||
| + | '''Intervalldaten bestehen aus gemessenen oder gezählten Werten, allerdings gibt es keine echte Null.''' Außerdem ist der Unterschied zwischen zwei Messwerten auf der Skala immer gleich groß, egal, wo man schaut. Das beste Beispiel ist die Temperatur, wenn man sie in °C misst. Der Unterschied zwischen 30°C und 40°C ist genauso groß wie der Unterschied zwischen 100°C und 110°C. Allerdings gibt es auf der Celsius-Skala keine echte Null: 0°C bedeutet nicht, dass es keine Temperatur gäbe. Stattdessen stellt 0°C einfach einen bestimmten Wert auf der Temperaturskala dar. Daher kann man Temperaturen zwar addieren und subtrahieren, aber nicht sinnvoll multiplizieren oder dividieren. Außerdem führt dieser Mangel einer echten Null dazu, dass 40°C nicht doppelt soviel Energie wie 20°C bedeutet, auch wenn die Zahl doppelt so groß ist. | ||
| + | |||
| + | |||
| + | === Qualitative Daten === | ||
| + | '''Qualitative (kategorische) Daten sind qualitative Daten, die in benannten Kategorien gesammelt werden können, die voneinander unabhängig sind.''' Solche Kategorien sind typischerweise konstruiert und enthalten daher Informationen, die zutiefst normativ sind. Ein Beispiel wäre die Haarfarbe, die in der menschlichen Wahrnehmung von Farben stattfinden kann, aber auch bei professionellen Haarprodukten oft mit unterschiedlichen Namen beschrieben wird. Innerhalb der Statistik werden Kategorien oft so gebildet, dass innerhalb eines wissenschaftlichen Experiments die Kategorien in einem Sinne konstruiert werden, der eine sinnvolle Prüfung der Hypothese ermöglicht, und sinnvoll liegt dann im Auge des Betrachters. Unterschiedliche Düngemittelmengen wären ein solches Beispiel, und die Kategorien werden oft auf Basis von Vorwissen oder Vortests gebildet. Kategorien sind also von besonderer Bedeutung, wenn es um die Reduzierung der Komplexität der Welt geht, da es nicht möglich wäre, alle möglichen unterschiedlichen Düngemittelmengen in einem Experiment zu testen. Stattdessen entscheidet man sich z.B. für "wenig", "moderat", "viel" und "sehr viel" Dünger. Dennoch muss man sich darüber im Klaren sein, dass - und wie - Kategorien konstruiert und damit zutiefst normativ sind. | ||
| + | |||
| + | Es gibt zwei Arten kategorischer Daten: ordinale und nominale Daten - und dann gibt es binäre Daten, die eigentlich nichts anderes sind als nominale Daten. | ||
| + | |||
| + | ==== Ordinale Daten ==== | ||
| + | [[File:Ordinal Data.jpg|thumb|right|'''Schulnoten sind ein anschauliches Beispiel für ordinale Daten.''']] | ||
| + | '''Ordinale Daten sind kategorische Daten, die in eine Reihenfolge gebracht werden können, mit denen sich aber nicht rechnen lässt, selbst wenn sie als Zahlen ausgedrückt werden.''' Erinnern Sie sich an Ihre Schulnoten? Eine "1" ist die beste Note im deutschen Notensystem, aber ist sie doppelt so gut wie eine "2"? Wohl kaum. Solche Noten sind [http://intellspot.com/nominal-vs-ordinal-data/ ordinale Zahlen]. Es handelt sich dabei um ein System von Zahlen, die in gewisser Weise geordnet sind, aber die Zahlen an sich spiegeln nicht unbedingt ein numerisches System wider. Mit anderen Worten: Sie sind höchst normativ und umstritten. Eine "2" mag für die einen eine gute Note sein, für die anderen eine Katastrophe. Ordinale Formate sind oft klar definierte Skalen, die es Menschen ermöglichen, bestimmte Informationen zu benoten, zu bewerten oder in eine Rangfolge zu bringen. Eines der bekanntesten Beispiele ist die [[Likert Scale|Likert-Skala]], die häufig in der Psychologie verwendet wird. In diesem Fall wird die Skalierung oft gar nicht in Zahlen wiedergegeben, sondern in Stufen wie "stimme voll zu" oder "stimme eher nicht zu". Solche konstruierten Skalen können echte Statistiker*innen sehr unglücklich machen, da die Ergebnisse schwer zu analysieren sind, aber es gibt kaum eine Alternative, da es auch keinen Sinn macht, zu fragen: "Wie glücklich sind Sie auf einer Skala von 1 bis 100?" Daher sind Ordinalskalen oft relevant, um ein Skalensystem zu schaffen, das eine breite Vergleichbarkeit ermöglicht oder sogar zu einer Norm wird, wie z.B. Schulnoten. Mein Rat wäre, [https://sciencing.com/advantages-disadvantages-using-ordinal-measurement-12043783.html Ordinalskalen zu verwenden], wenn dies in diesem Wissenschaftszweig üblich ist. Lesen Sie andere Studien auf dem Gebiet, und entscheiden Sie dann. Es handelt sich um hochgradig konstruierte Skalen, daher muss es eine klare Begründung geben, warum Sie sie verwenden wollen. | ||
====Nominale Daten==== | ====Nominale Daten==== | ||
| − | [[File: | + | [[File: Gummy Bears.jpg|thumb|right|Gummibärchen sind ein nettes Beispiel, da man sie nach ihrer Farbe klassifizieren kann, was nominale Daten wären. Aber wenn man sie wiegt, erhält man wieder kontinuierliche Daten.]] |
| − | Wann immer Sie | + | '''Wann immer Sie kategorische Daten haben, die nicht in eine Rangfolge gebracht werden können, nennt man sie [https://formpl.us/blog/nominal-data nominale Daten]'''. Ein Beispiel wären verschiedene Ethnien, Geburtsländer, oder verschiedene Arten von Geschlechtern. Dies verdeutlicht bereits, dass wir es hier mit oft völlig unterschiedlichen Weltanschauungen zu tun haben, sodass nominale Daten einen besonders starken Fall einer normativen Sicht auf die Welt darstellen. Das Geschlecht ist ein prominentes Beispiel, da manche Menschen das Geschlecht immer noch über ein biologisches Stereotyp (weiblich/männlich) und damit binär (siehe unten) definieren, was nach meinem Weltbild eindeutig falsch ist, weshalb ich Geschlecht nominal mit mehr als zwei Kategorien definieren würde. Nominale Datenformate verlangen daher eine noch deutlichere Reflexion als ordinale Daten, bei denen man zumindest sagen kann, dass eine bestimmte Schulnote höher ist als eine andere. Das ist bei nominalen Daten nicht der Fall. Deshalb muss man besonders vorsichtig sein mit den Implikationen, die eine bestimmte konstruierte Skala implizieren kann. |
| + | |||
| + | ====Binäre Daten==== | ||
| + | [[File: Mainzelmännchen-Ampel.png|200px|thumb|right|Ein Beispiel für Binärdaten]] | ||
| + | '''Binäre Daten sind das am meisten reduzierte Datenformat, das grundsätzlich aus zwei Ebenen besteht: 1 und 0'''. Streng genommen sind binäre Daten nominale Daten, aber eben nominale Daten, die nur in zwei Varianten vorliegen, die sich in 1 und 0 übersetzen lassen: An / Aus, Ja / Nein. In der [https://www.youtube.com/watch?v=ewokFOSxabs Informatik] werden binäre Daten direkt als einfache 0 und 1 genutzt, aber der große Durchbruch dieses Datensatzes kam schon früh in der Versicherungsbranche sowie in der Medizin, wo "tot" oder "lebendig" oft die grundlegendsten Fragen sind. Binäre Informationen sind eindeutig stark vereinfacht, was aber oft mit einer bestimmten Sicht der Realität übereinstimmt. Nehmen Sie das Beispiel, ein Instrument spielen zu können. Wenn Sie jemand fragt, ob Sie Klavier spielen können, werden Sie wahrscheinlich ''ja'' oder ''nein'' sagen. Sie werden Ihre Antwort höchstwahrscheinlich nicht qualifizieren, indem Sie sagen "Ich spiele besser als ein Affe, aber schlechter als Horowitz". Einige bescheidene Leute sagen vielleicht "Ich kann ein bisschen spielen", oder "Ich bin nicht sehr gut", oder "Ich war mal besser", aber sehr oft antworten Menschen mit ''ja'' oder ''nein''. Binäre Daten erlauben also eine vereinfachte Sicht auf die Realität, und diese mag oft mit der Welt übereinstimmen, wie wir sie wahrnehmen. Aber seien Sie sich bewusst: Andere Menschen haben vielleicht eine weniger einfache Sichtweise. | ||
| − | == | + | ==Die Auswahl des richtigen Datenformats== |
| − | + | Sie fragen sich jetzt vielleicht, wie Sie das richtige Datenformat auswählen. Die Antwort darauf ist ganz einfach. '''Jedes Datenformat sollte so einfach wie möglich und so komplex wie nötig sein.''' Folgen Sie Occams Rasiermesser, und Sie werden gut zurechtkommen. Das klingt natürlich verlockend, aber woher weiß man, was zu einfach und was zu komplex ist? Hier schlage ich vor, dass Sie sich auf die vorhandene Literatur stützen. Lesen Sie andere Veröffentlichungen, die ein bestimmtes Phänomen bereits untersucht haben, diese Veröffentlichungen können Ihnen bei der Wahl der richtigen Skala helfen. | |
| − | ==== | + | Die folgende Tabelle gibt Ihnen noch mehr Informationen über verschiedene Fatenformate - vielleicht hilft Sie Ihnen, Ihre Studie zu konzipieren? |
| − | [[File: | + | |
| − | + | [[File:Data Formats Table small 7.jpg|thumb|1000px|center|'''Verschiedene Datenformate und ihre Eigenschaften.''' Source: own]] | |
| + | |||
| + | ==Welcher einfache Test eignet sich für welches Datenformat?== | ||
| + | Die folgende Tabelle, die wir zusammengestellt haben, zeigt, welche statistischen Tests in Abhängigkeit von Ihren Daten sinnvoll sind. Um mehr über diese Tests zu erfahren, lesen Sie bitte die Einträge über [[Simple Statistical Tests|einfache statistische Tests]], [[Regression Analysis|Regressionsanalyse]], [[Correlations|Korrelationen]] und [[ANOVA]]. Hinweis: Für Kombinationen, die zu unterschiedlichen Methoden führen (z. B. ordinal x kontinuierlich), verweisen wir auf alle genannten Ansätze. | ||
| + | [[File:Table Simple Tests.png|600px|frameless|center|'''Welcher einfache Test eignet sich für welches Datenformat?''' Quelle: eigene Darstellung.]] | ||
| + | |||
| + | |||
| + | ==Ein Wort über Indizes== | ||
| + | In der Wirtschafts- und Finanzwelt ist ein Index ein statistisches Maß für die Veränderung einer repräsentativen Gruppe von einzelnen Datenpunkten. Ein gutes Beispiel für die Anwendung eines Indexes, den die meisten Menschen kennen, ist das [https://www.investopedia.com/terms/g/gdp.asp BIP], das Bruttoinlandsprodukt eines Landes. Obwohl es weitgehend kritisiert wurde, weil es zu allgemein gehalten ist und nicht genügend Nuancen bietet, um die Komplexität des einzelnen Landes zu verstehen, sind viele soziale, wirtschaftliche und andere Indikatoren mit dem BIP korreliert. | ||
| + | [[File:Bildschirmfoto 2020-04-11 um 11.24.41.png|thumb| Indizes erscheinen auch in unserem Alltag, wie ein Bild der neuesten Entwicklungen an der Börse.]] | ||
| + | In der Ökologie ist ein bekanntes Beispiel für einen Index der so genannte [https://www.youtube.com/watch?v=ghhZClDRK_g Shannon Wiener index], der Diversitätsmaße darstellt, welche hinsichtlich der Häufigkeit bestimmter Spezies angepasst sind. Ein prominentes Beispiel aus der Wirtschaft ist wiederum der [https://www.youtube.com/watch?v=_PXFVNWINQc Dow Jones index], während der [http://hdr.undp.org/en/content/human-development-index-hdi Index der menschlichen Entwicklung] versucht, Informationen über Lebenserwartung, Bildung und Einkommen zu integrieren, um ein allgemeines Verständnis für verschiedene Komponenten zu erhalten, die Länder charakterisieren. Der [https://www.investopedia.com/terms/g/gini-index.asp GINI-Koeffizient] versucht, die Ungleichheit zu messen, was sicherlich ein gewagtes Unterfangen ist, aber dennoch sehr wichtig. In der Psychologie ist der [https://www.youtube.com/watch?v=7p2a9B35Xn0 Intelligenzquotient], der natürlich stark kritisiert wird, ein bekanntes Beispiel für die Reduzierung vieler komplexer Tests auf eine Gesamtzahl. Indizes und Quotienten sind also Konstrukte, die oft auf vielen Variablen beruhen und versuchen, die Komplexität dieser vielfältigen Indikatoren auf eine einzige Zahl zu reduzieren. | ||
| + | |||
| + | |||
| + | ==Weitere Informationen== | ||
| + | ====Videos==== | ||
| + | [https://www.youtube.com/watch?v=7p2a9B35Xn0 Intelligence Quotient]: Answering the question if the IQ really measures how smart you are | ||
| + | |||
| + | [https://www.youtube.com/watch?v=hZxnzfnt5v8 Different data formats]: An overview | ||
| + | |||
| + | [https://www.youtube.com/watch?v=ewokFOSxabs Binary data]: How our computer works | ||
| + | |||
| + | [https://www.youtube.com/watch?v=ghhZClDRK_g The Shannon Wiener index]: An example from ecology | ||
| + | |||
| + | [https://www.youtube.com/watch?v=_PXFVNWINQc The Dow Jones Index]: An example from economy | ||
| + | |||
| + | [https://www.youtube.com/watch?v=7p2a9B35Xn0 The Intelligence Quotient]: A critical reflection | ||
| + | |||
| + | [https://www.youtube.com/watch?v=h8EYEJ32oQ8&list=PLU5aQXLWR3_yYS0ZYRA-5g5YSSYLNZ6Mc Descriptive Statistics]: A whole video series about descriptive statistics from the Khan academy | ||
| + | |||
| + | [https://www.youtube.com/watch?v=MRqtXL2WX2M Standard Deviation]: A brief explanation | ||
| + | |||
| + | [https://www.youtube.com/watch?v=mk8tOD0t8M0 Mode, Median, Mean, Range & Standard Deviation]: A good summary | ||
| + | |||
| + | [https://www.youtube.com/watch?v=bAU1MLRwh7c Back-of-envelope office space conundrum]: A real life example | ||
| + | |||
| + | ====Articles==== | ||
| + | [https://www.factmonster.com/math-science/weights-measures/metric-weights-and-measures Measurement]: Reflecting upon different measurement systems across the globe | ||
| + | |||
| + | [https://www.iqmindware.com/wiki/what-does-my-iq-score-mean IQ]: An explanation | ||
| + | |||
| + | [http://intellspot.com/nominal-vs-ordinal-data/ Nominal vs. ordinal data]: A comparison | ||
| + | |||
| + | [https://www.simplypsychology.org/likert-scale.html Likert scale]: The most popular rating scale | ||
| + | |||
| + | [https://sciencing.com/advantages-disadvantages-using-ordinal-measurement-12043783.html Ordinal data]: Limitations | ||
| + | |||
| + | [https://formpl.us/blog/nominal-data Nominal data]: An explanation | ||
| + | |||
| + | [https://en.wikipedia.org/wiki/Binary_data Binary data]: An explanation | ||
| + | |||
| + | [https://www.investopedia.com/terms/g/gdp.asp GDP]: A detailed article | ||
| + | |||
| + | [http://hdr.undp.org/en/content/human-development-index-hdi The Human Development Index]: An alternative to the GDP | ||
| + | |||
| + | [https://www.investopedia.com/terms/g/gini-index.asp The GINI index]: A measure of inequality | ||
| + | |||
| + | [https://www.investopedia.com/terms/d/descriptive_statistics.asp Descriptive Statistics]: An introduction | ||
| + | |||
| + | [http://intellspot.com/descriptive-statistics-examples/ Descriptive Statistics]: A detailed summary | ||
| + | |||
| + | [https://www.investopedia.com/terms/b/back-of-the-envelope-calculation.asp Back of the Envelope Calculation]: An explanation | ||
| − | + | [https://www.stlouisfed.org/on-the-economy/2020/march/back-envelope-estimates-next-quarters-unemployment-rate Estimates of Next Quarter’s Unemployment Rate]: An Example For Back of the Envelope Statistics | |
| − | + | ---- | |
| + | [[Category:Statistics]] | ||
| − | + | The [[Table of Contributors|author]] of this entry is Henrik von Wehrden. | |
| − | [[ | ||
Latest revision as of 16:09, 28 November 2023
Note: This is the German version of this entry. The original, English version can be found here: Data formats. This entry was translated using DeepL and only adapted slightly. Any etymological discussions should be based on the English text.
Kurz und knapp: Dieser Eintrag stellt unterschiedliche Datenformate vor.
Contents
Datenformate in der Statistik
Das Format Ihrer Daten beeinflusst alles Andere, was Sie im weiteren Verlauf Ihrer Arbeit tun. Um ein Sprichwort zu paraphrasieren: Die Daten haben ein Format, und das Format sind die Daten. Deshalb ist es wichtig zu wissen, welche verschiedenen Datenformate es gibt, und wie diese von Vorteil sein können, und wo Sie auf Probleme stoßen können. Weitere Informationen zu verschiedenen Messmethoden finden Sie im Eintrag To Rule And To Measure (German).
Der wichtigste Unterschied besteht zwischen quantitativen Daten und qualitativen Daten. Quantitative Daten können aus kontinuierlichen Daten, Intervalldaten und diskreten Daten bestehen, während qualitative Daten faktoriell - d. h. in wirklich verschiedenen Kategorien -, nominal oder ordinal sein können, wobei die beiden letzteren eine Verbindung zu quantitativen Daten herstellen. Die Nomenklatur für Datenformate ist jedoch in den verschiedenen Wissenschaftsbereichen sehr unterschiedlich, und um ehrlich zu sein, ein einziges Durcheinander. Wir versuchen hier, konsistent zu sein, aber seien Sie sich bitte bewusst, dass diese Bezeichnungen in der Wissenschaft nicht einheitlich sind.
Ein Beispiel für verschiedene Datenformate
Stellen Sie sich vor, Sie wollen Ihre Ernährung tracken. Viele Menschen tun dies heute, es gibt überall Ernährungsbücher und -ratgeber, viele Informationen sind verfügbar geworden. Nun möchten Sie damit beginnen und sich mit dem, was Sie essen, besser vertraut machen. Wie würden Sie anfangen? Mit dem Zählen von Kalorien? Unterscheiden Sie zwischen Kohlenhydraten, Fett und Gemüse? Vielleicht zählen Sie einfach jedes Mal, wenn Sie eine Pizza gegessen haben? Oder Eiscreme? Oder "zu viel"? Es gibt viele Möglichkeiten, Ihre Ernährung zu messen. Und diese Messungen können in verschiedenen Datenformaten erfolgen.
Die meisten Datenformate können in andere Datenformate umgewandelt werden, was für viele Menschen oft verwirrend ist. Zum Beispiel können nominale Daten wiederholt gezählt werden, z. B. die verschiedenen Tassen Kaffee, die Sie jeden Tag trinken, wie ein Flat White und zwei Espressi. Die Anzahl der Tassen würde sich dann aufaddieren, was diskrete Daten darstellen würde. Ein anderes Beispiel wären die Körpergrößen von Menschen, die als kontinuierliche Daten in Metern dargestellt werden könnte. Dieses kann zwar in Zahlen dargestellt werden, aber auch in Kategorien, wie "klein" und "groß".
Quantitative Daten
Quantitative (numerische) Daten sind Daten, die in Zahlen ausgedrückt werden, mit denen sich rechnen lässt. Es gibt drei Arten numerischer Daten: Kontinuierliche und diskrete Daten, sowie Intervalldaten.
Kontinuierliche Daten
Kontinuierliche Daten sind numerische Daten die nicht gezählt werden können, weil sie auf einer endlichen oder unendlichen Skala existieren. Wir alle sind mit kontinuierlichen Zahlen vertraut. Ein Großteil unserer Gesellschaft wird von diesen Zahlen beherrscht, und daher wird ein Großteil der in der Statistik analysierten Daten durch kontinuierliche Zahlen dargestellt. Da ein Großteil der modernen Messungen innerhalb eines vorgegebenen Systems automatisiert ist, müssen wir uns oft nicht allzu viele Gedanken darüber machen, wie die Daten aussehen. Nehmen Sie zum Beispiel Gewicht oder Größe. Innerhalb von Mitteleuropa wird dies eindeutig in Gramm oder Kilogramm bzw. in Zentimetern oder Metern gemessen. Wenn Sie jedoch in die USA ziehen, wird es eine ganz andere Geschichte, wegen des metrischen Systems, oder eher dessen mangelnder Nutzung. Plötzlich sind Sie einige Fuß groß und wiegen vielleicht einige "stones". Es gibt viele verschiedene Messsysteme, und man muss sich bewusst sein, wie diese genutzt werden. Diese Systeme sind also Konstrukte, und diese Konstrukte bauen auf kontinuierlichen Zahlen auf. Dies zeigt, dass kontinuierliche Zahlen weit verbreitet sind, um Daten auszudrücken, aber wir müssen uns bewusst sein, dass es sich dabei immer noch um normative Informationen handelt.
Kontinuierliche Daten haben eine echte Null. Eine echte Null ist definiert als völlige Abwesenheit von etwas, das in Zahlen dargestellt werden kann. Obwohl ein Gewicht von 0 kg oder eine Länge von 0 m abstrakt sind, stellen die Werte die Abwesenheit von Gewicht bzw. Länge dar.
Beispiele für kontinuierliche Daten:
- die Zahl Pi: 3,14159265359...
- das typische Gewicht einer Nacktmullratte: 30 Gramm
- die Höhe des Empire State Buildings: 443,2m
Diskrete Daten
Diskrete Daten sind numerische Daten, die gezählt werden können, da sie nur als natürliche Zahlen (1, 2, 3, 4...) vorliegen. Beispiele hierfür sind Schüler*innen in einer Klasse, oder das eigene Alter. Hier ergibt es keinen Sinn, mit kontinuierlichen Daten zu arbeiten. Natürlich kann man auch an einen halbierten Apfel denken, aber wenn wir Äpfel, Vögel oder Studierende zählen, betrachten wir sie normalerweise als vollständige Einheiten und halten uns an natürliche Zahlen. Diskrete Daten werden oft auch als "Häufigkeits-" oder "Zähldaten" bezeichnet, und in der Sprache R werden sie als "integer" (Ganzzahlen) bezeichnet.
Diskrete Daten haben auch eine echte Null. Nehmen wir noch einmal die Anzahl der Studierenden in einer Statistikvorlesung. Auch wenn die Vorlesung gut ist, zum Beispiel weil sie Lieder aus der Sesamstraße enthält, kann es sein, dass keine Studierenden in der Vorlesung sind. 0 Studierende in einer Vorlesung - da haben Sie Ihre echte Null.
Intervalldaten
Intervalldaten bestehen aus gemessenen oder gezählten Werten, allerdings gibt es keine echte Null. Außerdem ist der Unterschied zwischen zwei Messwerten auf der Skala immer gleich groß, egal, wo man schaut. Das beste Beispiel ist die Temperatur, wenn man sie in °C misst. Der Unterschied zwischen 30°C und 40°C ist genauso groß wie der Unterschied zwischen 100°C und 110°C. Allerdings gibt es auf der Celsius-Skala keine echte Null: 0°C bedeutet nicht, dass es keine Temperatur gäbe. Stattdessen stellt 0°C einfach einen bestimmten Wert auf der Temperaturskala dar. Daher kann man Temperaturen zwar addieren und subtrahieren, aber nicht sinnvoll multiplizieren oder dividieren. Außerdem führt dieser Mangel einer echten Null dazu, dass 40°C nicht doppelt soviel Energie wie 20°C bedeutet, auch wenn die Zahl doppelt so groß ist.
Qualitative Daten
Qualitative (kategorische) Daten sind qualitative Daten, die in benannten Kategorien gesammelt werden können, die voneinander unabhängig sind. Solche Kategorien sind typischerweise konstruiert und enthalten daher Informationen, die zutiefst normativ sind. Ein Beispiel wäre die Haarfarbe, die in der menschlichen Wahrnehmung von Farben stattfinden kann, aber auch bei professionellen Haarprodukten oft mit unterschiedlichen Namen beschrieben wird. Innerhalb der Statistik werden Kategorien oft so gebildet, dass innerhalb eines wissenschaftlichen Experiments die Kategorien in einem Sinne konstruiert werden, der eine sinnvolle Prüfung der Hypothese ermöglicht, und sinnvoll liegt dann im Auge des Betrachters. Unterschiedliche Düngemittelmengen wären ein solches Beispiel, und die Kategorien werden oft auf Basis von Vorwissen oder Vortests gebildet. Kategorien sind also von besonderer Bedeutung, wenn es um die Reduzierung der Komplexität der Welt geht, da es nicht möglich wäre, alle möglichen unterschiedlichen Düngemittelmengen in einem Experiment zu testen. Stattdessen entscheidet man sich z.B. für "wenig", "moderat", "viel" und "sehr viel" Dünger. Dennoch muss man sich darüber im Klaren sein, dass - und wie - Kategorien konstruiert und damit zutiefst normativ sind.
Es gibt zwei Arten kategorischer Daten: ordinale und nominale Daten - und dann gibt es binäre Daten, die eigentlich nichts anderes sind als nominale Daten.
Ordinale Daten
Ordinale Daten sind kategorische Daten, die in eine Reihenfolge gebracht werden können, mit denen sich aber nicht rechnen lässt, selbst wenn sie als Zahlen ausgedrückt werden. Erinnern Sie sich an Ihre Schulnoten? Eine "1" ist die beste Note im deutschen Notensystem, aber ist sie doppelt so gut wie eine "2"? Wohl kaum. Solche Noten sind ordinale Zahlen. Es handelt sich dabei um ein System von Zahlen, die in gewisser Weise geordnet sind, aber die Zahlen an sich spiegeln nicht unbedingt ein numerisches System wider. Mit anderen Worten: Sie sind höchst normativ und umstritten. Eine "2" mag für die einen eine gute Note sein, für die anderen eine Katastrophe. Ordinale Formate sind oft klar definierte Skalen, die es Menschen ermöglichen, bestimmte Informationen zu benoten, zu bewerten oder in eine Rangfolge zu bringen. Eines der bekanntesten Beispiele ist die Likert-Skala, die häufig in der Psychologie verwendet wird. In diesem Fall wird die Skalierung oft gar nicht in Zahlen wiedergegeben, sondern in Stufen wie "stimme voll zu" oder "stimme eher nicht zu". Solche konstruierten Skalen können echte Statistiker*innen sehr unglücklich machen, da die Ergebnisse schwer zu analysieren sind, aber es gibt kaum eine Alternative, da es auch keinen Sinn macht, zu fragen: "Wie glücklich sind Sie auf einer Skala von 1 bis 100?" Daher sind Ordinalskalen oft relevant, um ein Skalensystem zu schaffen, das eine breite Vergleichbarkeit ermöglicht oder sogar zu einer Norm wird, wie z.B. Schulnoten. Mein Rat wäre, Ordinalskalen zu verwenden, wenn dies in diesem Wissenschaftszweig üblich ist. Lesen Sie andere Studien auf dem Gebiet, und entscheiden Sie dann. Es handelt sich um hochgradig konstruierte Skalen, daher muss es eine klare Begründung geben, warum Sie sie verwenden wollen.
Nominale Daten
Wann immer Sie kategorische Daten haben, die nicht in eine Rangfolge gebracht werden können, nennt man sie nominale Daten. Ein Beispiel wären verschiedene Ethnien, Geburtsländer, oder verschiedene Arten von Geschlechtern. Dies verdeutlicht bereits, dass wir es hier mit oft völlig unterschiedlichen Weltanschauungen zu tun haben, sodass nominale Daten einen besonders starken Fall einer normativen Sicht auf die Welt darstellen. Das Geschlecht ist ein prominentes Beispiel, da manche Menschen das Geschlecht immer noch über ein biologisches Stereotyp (weiblich/männlich) und damit binär (siehe unten) definieren, was nach meinem Weltbild eindeutig falsch ist, weshalb ich Geschlecht nominal mit mehr als zwei Kategorien definieren würde. Nominale Datenformate verlangen daher eine noch deutlichere Reflexion als ordinale Daten, bei denen man zumindest sagen kann, dass eine bestimmte Schulnote höher ist als eine andere. Das ist bei nominalen Daten nicht der Fall. Deshalb muss man besonders vorsichtig sein mit den Implikationen, die eine bestimmte konstruierte Skala implizieren kann.
Binäre Daten
Binäre Daten sind das am meisten reduzierte Datenformat, das grundsätzlich aus zwei Ebenen besteht: 1 und 0. Streng genommen sind binäre Daten nominale Daten, aber eben nominale Daten, die nur in zwei Varianten vorliegen, die sich in 1 und 0 übersetzen lassen: An / Aus, Ja / Nein. In der Informatik werden binäre Daten direkt als einfache 0 und 1 genutzt, aber der große Durchbruch dieses Datensatzes kam schon früh in der Versicherungsbranche sowie in der Medizin, wo "tot" oder "lebendig" oft die grundlegendsten Fragen sind. Binäre Informationen sind eindeutig stark vereinfacht, was aber oft mit einer bestimmten Sicht der Realität übereinstimmt. Nehmen Sie das Beispiel, ein Instrument spielen zu können. Wenn Sie jemand fragt, ob Sie Klavier spielen können, werden Sie wahrscheinlich ja oder nein sagen. Sie werden Ihre Antwort höchstwahrscheinlich nicht qualifizieren, indem Sie sagen "Ich spiele besser als ein Affe, aber schlechter als Horowitz". Einige bescheidene Leute sagen vielleicht "Ich kann ein bisschen spielen", oder "Ich bin nicht sehr gut", oder "Ich war mal besser", aber sehr oft antworten Menschen mit ja oder nein. Binäre Daten erlauben also eine vereinfachte Sicht auf die Realität, und diese mag oft mit der Welt übereinstimmen, wie wir sie wahrnehmen. Aber seien Sie sich bewusst: Andere Menschen haben vielleicht eine weniger einfache Sichtweise.
Die Auswahl des richtigen Datenformats
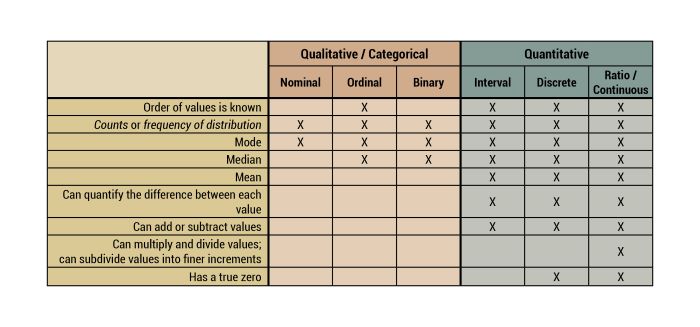
Sie fragen sich jetzt vielleicht, wie Sie das richtige Datenformat auswählen. Die Antwort darauf ist ganz einfach. Jedes Datenformat sollte so einfach wie möglich und so komplex wie nötig sein. Folgen Sie Occams Rasiermesser, und Sie werden gut zurechtkommen. Das klingt natürlich verlockend, aber woher weiß man, was zu einfach und was zu komplex ist? Hier schlage ich vor, dass Sie sich auf die vorhandene Literatur stützen. Lesen Sie andere Veröffentlichungen, die ein bestimmtes Phänomen bereits untersucht haben, diese Veröffentlichungen können Ihnen bei der Wahl der richtigen Skala helfen.
Die folgende Tabelle gibt Ihnen noch mehr Informationen über verschiedene Fatenformate - vielleicht hilft Sie Ihnen, Ihre Studie zu konzipieren?
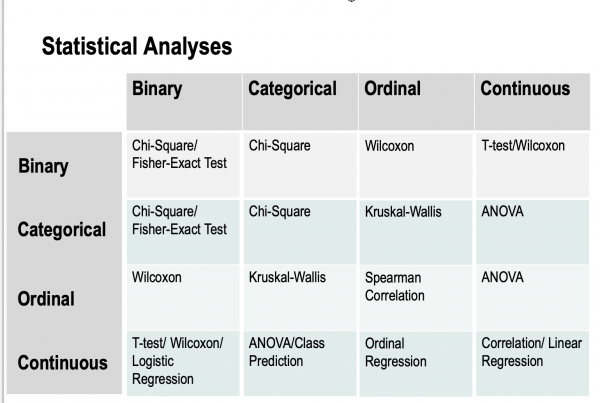
Welcher einfache Test eignet sich für welches Datenformat?
Die folgende Tabelle, die wir zusammengestellt haben, zeigt, welche statistischen Tests in Abhängigkeit von Ihren Daten sinnvoll sind. Um mehr über diese Tests zu erfahren, lesen Sie bitte die Einträge über einfache statistische Tests, Regressionsanalyse, Korrelationen und ANOVA. Hinweis: Für Kombinationen, die zu unterschiedlichen Methoden führen (z. B. ordinal x kontinuierlich), verweisen wir auf alle genannten Ansätze.
Ein Wort über Indizes
In der Wirtschafts- und Finanzwelt ist ein Index ein statistisches Maß für die Veränderung einer repräsentativen Gruppe von einzelnen Datenpunkten. Ein gutes Beispiel für die Anwendung eines Indexes, den die meisten Menschen kennen, ist das BIP, das Bruttoinlandsprodukt eines Landes. Obwohl es weitgehend kritisiert wurde, weil es zu allgemein gehalten ist und nicht genügend Nuancen bietet, um die Komplexität des einzelnen Landes zu verstehen, sind viele soziale, wirtschaftliche und andere Indikatoren mit dem BIP korreliert.
In der Ökologie ist ein bekanntes Beispiel für einen Index der so genannte Shannon Wiener index, der Diversitätsmaße darstellt, welche hinsichtlich der Häufigkeit bestimmter Spezies angepasst sind. Ein prominentes Beispiel aus der Wirtschaft ist wiederum der Dow Jones index, während der Index der menschlichen Entwicklung versucht, Informationen über Lebenserwartung, Bildung und Einkommen zu integrieren, um ein allgemeines Verständnis für verschiedene Komponenten zu erhalten, die Länder charakterisieren. Der GINI-Koeffizient versucht, die Ungleichheit zu messen, was sicherlich ein gewagtes Unterfangen ist, aber dennoch sehr wichtig. In der Psychologie ist der Intelligenzquotient, der natürlich stark kritisiert wird, ein bekanntes Beispiel für die Reduzierung vieler komplexer Tests auf eine Gesamtzahl. Indizes und Quotienten sind also Konstrukte, die oft auf vielen Variablen beruhen und versuchen, die Komplexität dieser vielfältigen Indikatoren auf eine einzige Zahl zu reduzieren.
Weitere Informationen
Videos
Intelligence Quotient: Answering the question if the IQ really measures how smart you are
Different data formats: An overview
Binary data: How our computer works
The Shannon Wiener index: An example from ecology
The Dow Jones Index: An example from economy
The Intelligence Quotient: A critical reflection
Descriptive Statistics: A whole video series about descriptive statistics from the Khan academy
Standard Deviation: A brief explanation
Mode, Median, Mean, Range & Standard Deviation: A good summary
Back-of-envelope office space conundrum: A real life example
Articles
Measurement: Reflecting upon different measurement systems across the globe
IQ: An explanation
Nominal vs. ordinal data: A comparison
Likert scale: The most popular rating scale
Ordinal data: Limitations
Nominal data: An explanation
Binary data: An explanation
GDP: A detailed article
The Human Development Index: An alternative to the GDP
The GINI index: A measure of inequality
Descriptive Statistics: An introduction
Descriptive Statistics: A detailed summary
Back of the Envelope Calculation: An explanation
Estimates of Next Quarter’s Unemployment Rate: An Example For Back of the Envelope Statistics
The author of this entry is Henrik von Wehrden.