Difference between revisions of "Simple Statistical Tests"
| Line 47: | Line 47: | ||
'''Example:''' An easy example would be the behaviour of nesting birds. The range of birds outside of the breedig season dramatcally differs from the range when they are nesting. | '''Example:''' An easy example would be the behaviour of nesting birds. The range of birds outside of the breedig season dramatcally differs from the range when they are nesting. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 66: | Line 60: | ||
For this example, the chi-quare test yields a p-value of 2.439e-07, which is close to zero. We can reject the null hypothesis H0 and assume that, based on our sample, the education of parents has an influence on the education of their children. | For this example, the chi-quare test yields a p-value of 2.439e-07, which is close to zero. We can reject the null hypothesis H0 and assume that, based on our sample, the education of parents has an influence on the education of their children. | ||
| + | |||
| + | |||
| + | ====Wilcoxon Test==== | ||
| + | '''The next important test is the [https://data.library.virginia.edu/the-wilcoxon-rank-sum-test/ Wilcoxon rank sum test]'''. This test is also a paired test. What is most relevant here is that not the real numbers are introduced into the calculation, but instead these numbers are transformed into ranks. In other words, you get rid of the question about normal distribution and instead reduce your real numbers to an order of numbers. This can come in handy when you have very skewed distribution - so a exceptionally non-normal distribution - or large gaps in your data. The test will tell you if the means of two samples differ significantly (i.e. p-value below 0,05) by using ranks. | ||
| + | |||
| + | '''Example:''' An example would be the comparison in growths of young people compared to their size as adults. Imagine you have a sample where half of your people are professional basketball players then the real size of people would not make sense. Therefore, as a robust measure in modern statistics, rank tests were introduced. | ||
| Line 72: | Line 72: | ||
[[File:NormalDistribution2.png|thumb|right|Figure 2. Source: [https://commons.wikimedia.org/wiki/File:NormalDist.png Wikipedia]]] | [[File:NormalDistribution2.png|thumb|right|Figure 2. Source: [https://commons.wikimedia.org/wiki/File:NormalDist.png Wikipedia]]] | ||
| − | The f-test allows you to compare the '' | + | The f-test allows you to compare the ''variance'' of two samples. Variance is calculated by taking the average of squared deviations from the mean and tells you the degree of spread in your data set. The more spread the data, the larger the variance is in relation to the mean. If the p-value of the f-test is lower than 0,05, the variances differ significantly. |
'''Example''': If you examine players in a basketball and a hockey team, you would expect their heights to be different on average. But maybe the variance is not. Consider figure no. 1, where the mean is different, but the variance the same - this could be the case for your hockey and basketball team. In contrast, the height could be distributed as shown in figure no. 2. The f-test then would probably yield a p-value below 0,05. | '''Example''': If you examine players in a basketball and a hockey team, you would expect their heights to be different on average. But maybe the variance is not. Consider figure no. 1, where the mean is different, but the variance the same - this could be the case for your hockey and basketball team. In contrast, the height could be distributed as shown in figure no. 2. The f-test then would probably yield a p-value below 0,05. | ||
| Line 172: | Line 172: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| + | |||
| + | ==== Chi Square Test ==== | ||
| + | <syntaxhighlight lang="R" line> | ||
| + | |||
| + | #-------CHI-SQUARE TEST EXAMPLE------- | ||
| + | |||
| + | #For analysis, data was taken from the Statistisches Bundesamt site. | ||
| + | #This is data of smoking habits by sex for age-groups from 30 to 35. | ||
| + | #We want to know if there is a relationship between gender and smoking habits. | ||
| + | #H0:there is no dependence between signs | ||
| + | #H1:there is a dependency | ||
| + | |||
| + | #Create data table | ||
| + | SmokingHabits <- as.table(rbind(c(162,824,414,1295), c(127,511,449,1495))) | ||
| + | dimnames(SmokingHabits) <- list(gender = c("Male", "Female"), | ||
| + | habits = c("occasional","regular","previous_smoker","never_smoking")) | ||
| + | |||
| + | #Chi-Square Test | ||
| + | chisq.test(SmokingHabits) # Prints test summary | ||
| + | |||
| + | #(p-value < 0.05) -> Reject hypothesis H0 -> Signs depend. Smoking habits substantially depends on gender. | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | |||
| + | === Wilcoxon Test ==== | ||
| + | <syntaxhighlight lang="R" line> | ||
| + | #---------------------------Wilcoxon rank sum test------------------------------------- | ||
| + | #We want to analyse the iris Dataset provided by R | ||
| + | iris <- iris | ||
| + | |||
| + | #Lets have a first look on the Data | ||
| + | head(iris) | ||
| + | str(iris) | ||
| + | summary(iris) | ||
| + | #The dataset gives the measurements in centimeters of the variables sepal length and width | ||
| + | #and petal length and width, | ||
| + | #respectively, for 50 flowers from each of 3 species of iris. | ||
| + | #The species are Iris setosa, versicolor, and virginica. | ||
| + | |||
| + | #lets split the dataset into 3 datasets for each species | ||
| + | versicolor <- subset(iris, Species == "versicolor") | ||
| + | virginica <- subset(iris, Species == "virginica") | ||
| + | setosa <- subset(iris, Species == "setosa") | ||
| + | |||
| + | #Now we can for example test, if the difference in sepal length between setosa and virginica is significant: | ||
| + | #H0 hypothesis: The medians (distributions) of setosa and virginica are equal | ||
| + | #H1 hypothesis: The medians (distributions) of setosa and virginica differ | ||
| + | |||
| + | #test for normality | ||
| + | shapiro.test(setosa$Sepal.Length) | ||
| + | shapiro.test(virginica$Sepal.Length) | ||
| + | #both are not normally distributed | ||
| + | |||
| + | #wilcoxon sum of ranks test | ||
| + | wilcox.test(setosa$Sepal.Length,virginica$Sepal.Length) | ||
| + | |||
| + | #the p-value is 2.2e-16, which is below 0.05 (it's almost 0). | ||
| + | #Therefore we neglect the H0 Hypothesis and adopt the H1 Hypothesis. | ||
| + | #Based on this result we may conclude the medians of these two distributions differ. | ||
| + | #The alternative hypothesis is stated as the “true location shift is not equal to 0”. | ||
| + | #That’s another way of saying “the distribution of one population is shifted to the left or | ||
| + | #right of the other,” which implies different medians. | ||
| + | |||
| + | </syntaxhighlight> | ||
| + | |||
| + | |||
| + | ==== f-test ==== | ||
| + | ADD R EXAMPLE | ||
== Strengths & Challenges == | == Strengths & Challenges == | ||
Revision as of 06:15, 30 March 2021
| Method categorization | ||
|---|---|---|
| Quantitative | Qualitative | |
| Inductive | Deductive | |
| Individual | System | Global |
| Past | Present | Future |
In short: Simple statistical tests encapsule an array of simple statistical tests that are all built on probability, and no other validation criteria.
Contents
Background
Simple statistical tests statistics provide the baseline for advanced statistical thinking. While they are not so much used today within empirical analysis, simple tests are the foundation of modern statistics. The student t-test which originated around 100 years ago provided the crucial link from the more inductive thinking of Sir Francis Bacon towards the testing of hypotheses and the actual statistical testing of hypotheses. The formulation of the so-called null hypothesis is the first step within simple tests. Informed from theory this test calculates the probability whether the sample confirms the hypothesis or not. Null hypotheses are hence the assumptions we have about the world, and these assumptions can be confirmed or rejected.
Most relevant simple tests
Note: Examples for how to implement these tests in R are shown in the section below.
One sample t-test
The easiest example is the one sample t-test: it allows us to test a dataset (more specifically, its mean value) versus a specified value. For this purpose, the t-test gives you a p-value at the end. If the p-value is below 0.05, the sample differs significantly from the reference value.
Example: Do the packages of your favourite cookie brand always contain as many cookies as stated on the outside of the box? Collect some of the packages, weigh the cookies contained therein and calculate the mean weight. Now, you can compare this value to the weight that is stated on the box using a one sample t-test.
Two sample t-test
Two sample tests are the next step. These allow a comparison of two different datasets within an experiment. They tell you if the means of the two datasets differ significantly. If the p-value is below 0,05, the two datasets differ significantly. It is clear that the usefulness of this test widely depends on the number of samples - the more samples we have for each dataset, the more we can understand about the difference between the datasets
Example: The classic example would be to grow several plants and to add fertiliser to half of them. We can now compare the gross of the plants between the control samples without fertiliser and the samples that had fertiliser added.
Plants with fertiliser (cm): 7.44 6.35 8.52 11.40 10.48 11.23 8.30 9.33 9.55 10.40 8.36 9.69 7.66 8.87 12.89 10.54 6.72 8.83 8.57 7.75
Plants without fertiliser (cm): 6.07 9.55 5.72 6.84 7.63 5.59 6.21 3.05 4.32 8.27 6.13 7.92 4.08 7.33 9.91 8.35 7.26 6.08 5.81 8.46
The result of the two-sample t-test is a p-value of 7.468e-05, which is close to zero and definitely below 0,05. Hence, the samples differ significantly and the fertilizer is likely to have an effect.
Paired t-test
Paired t-tests are the third type of simple statistics. These allow for a comparison of a sample before and after an intervention. Within such an experimental setup, specific individuals are compared before and after an event. This way, the influence of the event on the dataset can be evaluated. If the sample changes significantly, comparing start and end state, you will receive again a p-value below 0,05.
Example: An easy example would be the behaviour of nesting birds. The range of birds outside of the breedig season dramatcally differs from the range when they are nesting.
Chi-square Test of Stochastic Independence
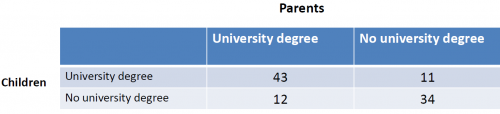
The Chi Square test works for data that is only categorical. If you observe an event and measure two variables, you can use the Chi Square test to check if one variable influences the other one or if they occur independently from each other.
Example: Do the children of parents with an academic degree visit more often a university?
The H0 hypothesis would be: The variables are independent from each other.
The H1 hypotheses would be: The variables influence each other. For example because children from better educated families have higher chances to achieve good results in school.
For this example, the chi-quare test yields a p-value of 2.439e-07, which is close to zero. We can reject the null hypothesis H0 and assume that, based on our sample, the education of parents has an influence on the education of their children.
Wilcoxon Test
The next important test is the Wilcoxon rank sum test. This test is also a paired test. What is most relevant here is that not the real numbers are introduced into the calculation, but instead these numbers are transformed into ranks. In other words, you get rid of the question about normal distribution and instead reduce your real numbers to an order of numbers. This can come in handy when you have very skewed distribution - so a exceptionally non-normal distribution - or large gaps in your data. The test will tell you if the means of two samples differ significantly (i.e. p-value below 0,05) by using ranks.
Example: An example would be the comparison in growths of young people compared to their size as adults. Imagine you have a sample where half of your people are professional basketball players then the real size of people would not make sense. Therefore, as a robust measure in modern statistics, rank tests were introduced.
f-test
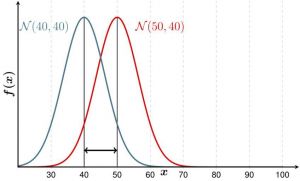
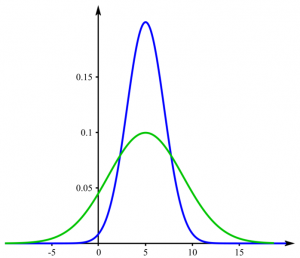
The f-test allows you to compare the variance of two samples. Variance is calculated by taking the average of squared deviations from the mean and tells you the degree of spread in your data set. The more spread the data, the larger the variance is in relation to the mean. If the p-value of the f-test is lower than 0,05, the variances differ significantly.
Example: If you examine players in a basketball and a hockey team, you would expect their heights to be different on average. But maybe the variance is not. Consider figure no. 1, where the mean is different, but the variance the same - this could be the case for your hockey and basketball team. In contrast, the height could be distributed as shown in figure no. 2. The f-test then would probably yield a p-value below 0,05.
R Examples
two-sample t-test
#---------------------------t-test------------------------------------- #The t-test can be used on interval data or ratio data to test if two samples of a population differ significantly. #Which is, that the samples have different means. #H0 hypothesis: The two samples' means are not different. #H1 hypothesis: The two samples' means are different. #---------------------------analysis------------------------------------- #We want to analyse the iris Dataset provided by R iris <- iris #Lets have a first look on the Data head(iris) str(iris) summary(iris) #The dataset gives the measurements in centimeters of the variables sepal length and width #and petal length and width, #respectively, for 50 flowers from each of 3 species of iris. #The species are Iris setosa, versicolor, and virginica. #lets split the dataset into 3 datasets for each species versicolor <- subset(iris, Species == "versicolor") virginica <- subset(iris, Species == "virginica") setosa <- subset(iris, Species == "setosa") #Now we can for example test, if the difference in petal length between versicolor and virginica is significant: #H0 hypothesis: versicolor and virginica do not have different petal length #H1 hypothesis: versicolor and virginica have different petal length #Let's check, what the t-test says. t.test(versicolor$Petal.Length,virginica$Petal.Length) #the p-value is 2.2e-16, which is below 0.05 (it's almost 0). #Therefore we neglect the H0 Hypothesis and adopt the H1 Hypothesis.
Paired t-test
# R Example for a Paired Samples T-Test # Paired Samples - when we apply the 2 treatments to the same samples, # giving us paired combinations of samples for the 2 treatments # Assumptions for the Paired Sample T-Test: # (1) Differences between paired values follow a Normal distribution # (2) Data is Continuous # (3) We have paired or dependent samples # (4) Simple Random Sampling - each unit has an equal probability of being selected # Setting up our Hypotheses (Two-Tailed): # H0: The pairwise difference between means is 0 / Paired Population Means are equal # H1: The pairwise difference between means is not 0 / Paired Population Means are not equal # Example: # Consider the supplement dataset to show the effect of 2 supplements on the time #it takes for an athlete (in minutes) to finish a practice race s1 <- c(10.9, 12.5, 11.4, 13.6, 12.2, 13.2, 10.6, 14.3, 10.4, 10.3) s2 <- c(15.7, 16.6, 18.2, 15.2, 17.8, 20.0, 14.0, 18.7, 16.0, 17.3) id <- c(1,2,3,4,5,6,7,8,9,10) supplement <- data.frame(id,s1,s2) supplement$difference <- supplement$s1 - supplement$s2 View(supplement) # Exploring the data summary(supplement) str(supplement) # Now, we can go for the Paired Samples T-Test # We can define our Hypotheses as (Two-Tailed): # H0: There is no significant difference in the mean time taken to finish the race # for the 2 supplements # H1: There is a significant difference in the mean time taken to finish the race # for the 2 supplements t.test(supplement$s1, supplement$s2, paired = TRUE) # As the p-value is less than the level of significance (0.05), we have # sufficient evidence to reject H0 and conclude that there is a significant # difference in the mean time taken to finish the race with the 2 supplements # Alternatively, if we wanted to check which supplement gives a better result, # we could use a one tailed test by changing the alternate argument to less or greater
Chi Square Test
#-------CHI-SQUARE TEST EXAMPLE-------
#For analysis, data was taken from the Statistisches Bundesamt site.
#This is data of smoking habits by sex for age-groups from 30 to 35.
#We want to know if there is a relationship between gender and smoking habits.
#H0:there is no dependence between signs
#H1:there is a dependency
#Create data table
SmokingHabits <- as.table(rbind(c(162,824,414,1295), c(127,511,449,1495)))
dimnames(SmokingHabits) <- list(gender = c("Male", "Female"),
habits = c("occasional","regular","previous_smoker","never_smoking"))
#Chi-Square Test
chisq.test(SmokingHabits) # Prints test summary
#(p-value < 0.05) -> Reject hypothesis H0 -> Signs depend. Smoking habits substantially depends on gender.
Wilcoxon Test =
#---------------------------Wilcoxon rank sum test------------------------------------- #We want to analyse the iris Dataset provided by R iris <- iris #Lets have a first look on the Data head(iris) str(iris) summary(iris) #The dataset gives the measurements in centimeters of the variables sepal length and width #and petal length and width, #respectively, for 50 flowers from each of 3 species of iris. #The species are Iris setosa, versicolor, and virginica. #lets split the dataset into 3 datasets for each species versicolor <- subset(iris, Species == "versicolor") virginica <- subset(iris, Species == "virginica") setosa <- subset(iris, Species == "setosa") #Now we can for example test, if the difference in sepal length between setosa and virginica is significant: #H0 hypothesis: The medians (distributions) of setosa and virginica are equal #H1 hypothesis: The medians (distributions) of setosa and virginica differ #test for normality shapiro.test(setosa$Sepal.Length) shapiro.test(virginica$Sepal.Length) #both are not normally distributed #wilcoxon sum of ranks test wilcox.test(setosa$Sepal.Length,virginica$Sepal.Length) #the p-value is 2.2e-16, which is below 0.05 (it's almost 0). #Therefore we neglect the H0 Hypothesis and adopt the H1 Hypothesis. #Based on this result we may conclude the medians of these two distributions differ. #The alternative hypothesis is stated as the “true location shift is not equal to 0”. #That’s another way of saying “the distribution of one population is shifted to the left or #right of the other,” which implies different medians.
f-test
ADD R EXAMPLE
Strengths & Challenges
(more to be added soon)
t-test
- The data of the sample(s) has to be normally distributed
- Dependend on the kind of t-test applied, the parent populations of the samples need to have the same variance (1)
Wilcoxon Test
Chi-square Test of Stochastical Independence
f-test
- The data of the samples has to be normally distributed
For more info on data distribution types, please refer to the entry on Data distribution.
Normativity
Simple tests are not abundantly applied these days in scientific research, and often seem outdated. Much of the scientific designs and available datasets are more complicated, and many branches of sciences established more complex designs and a more nuanced view of the world. Consequently, simple tests grew kind of out of fashion. However, simple tests are not only robust, but sometimes still the most parsimonious approach. In addition, many simple tests are a basis for more complicated approaches, and initiated a deeper and more applied starting point for frequentist statistics. Simple tests are often the endpoint of many introductionary teachings on statistics, which is unfortunate. Overall, their lack in most of recent publications as well as wooden design frames of these approaches make these tests an undesirable starting point for many students, yet they are a vital stepping stone to more advanced models.
Outlook
Hopefully, one day school children will learn simple test, because they could, and the world would be all the better for it. If more people early on would learn about probability, and simple tests are a stepping stone on this long road, there would be an education deeper rooted in data and analysis, allowing for better choices and understanding of citizens.
Key Publications
- Student" William Sealy Gosset. 1908. The probable error of a mean. Biometrika 6 (1). 1–25.
- Cochran, William G. 1952. The Chi-square Test of Goodness of Fit. The Annals of Mathematical Statistics 23 (3). 315–345.
- Box, G. E. P. 1953. Non-Normality and Tests on Variances. Biometrika 40 (3/4). 318–335.
References
(1) Article on the "Student's t-test" on Wikipedia
The authors of this entry are Henrik von Wehrden and Carlo Krügermeier.