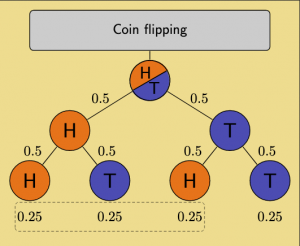
Data distribution
(The author of this entry is Henrik von Wehrden.)
Data distribution
Data distribution is the most basic and also fundamental step of analysis for any given data set. On the other hand, data distribution encompasses the most complex concepts in statistics, thereby including also a diversity of concepts that translates further into many different steps of analysis. Consequently, without understanding the basics of data distribution, it is next to impossible to understand any statistics down the road. Data distribution can be seen as the fundamentals, and we shall often return to these when building statistics further.
The normal distribution
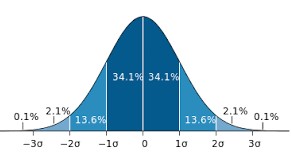
How wonderful, it is truly a miracle how almost everything that can be measured seems to be following the normal distribution. Overall, the normal distribution is not only the most abundantly occurring, but also the earliest distribution that was known. It follows the premise that most data in any given dataset has its majority around a mean value, and only small amounts of the data are found at the extremes.
Most phenomena we can observe follow a normal distribution. The fact that many do not want this to be true is I think associated to the fact that it makes us assume that the world is not complex, which is counterintuitive to many. While I believe that the world can be complex, there are many natural laws that explain many phenomena we investigate. The Gaussian normal distribution is such an example. Most things that can be measured in any sense (length, weight etc.) are normally distributed, meaning that if you measure many different items of the same thing, the data follows a normal distribution.
The easiest example is tallness of people. While there is a gender difference in terms of height, all people that would identify as e.g. females have a certain height. Most have a different height from each other, yet there are almost always many of a mean height, and few very small and few very tall females within a given population. There are of course exceptions, for instance due to selection biases. The members of a professional basketball team would for instance follow a selection bias, as these would need to be ideally tall. Within the normal population, people’s height follow the normal distribution. The same holds true for weight, and many other things that can be measured.
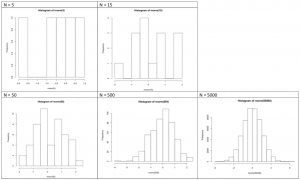
Most things in their natural state follow a normal distribution. If somebody tells you that something is not normally distributed, this person is either very clever or not very clever. A small sample can hamper you from finding a normal distribution. If you weight five people you will hardly find a normal distribution, as the sample is obviously too small. While it may seem like a magic trick, it is actually true that many phenomena that can be measured will follow the normal distribution, at least when your sample is large enough. Consequently, much of the probabilistic statistics is built on the normal distribution.
The most abundant reason for a deviance from the normal distribution is us. We changed the planet and ourselves, creating effects that may change everything, up to the normal distribution. Take weight. Today the human population shows a very complex pattern in terms of weight distribution across the globe, and there are many reasons why the weight distribution does not follow a normal distribution. There is no such thing as a normal weight, but studies from indigenous communities show a normal distribution in the weight found in their populations. Within our wider world, this is clearly different. Yet before we bash the western diet, please remember that never before in the history of humans did we have a more steady stream of calories, which is not all bad.
Skew of distributions
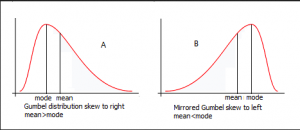
Apart from that distributions can have different skews. There is the symmetrical skew which is basically a normal distributions or bell curve that you can see on the picture. But normal distributions can also be skewed to the left or to the right depending on how mode, median and mean differ. For the symmetrical normal distribution they are of course all the same but for the right skewed distribution (mode < median < mean) it's different.
See Tests for normal distribution to learn how to check if the data is normally distributed.
Detecting the normal distribution
But when is data normally distributed and how to recognize it when you have a boxplot in front of you? Or a histogram? The best way to learn it, is to look at it. Always remember the ideal picture of the bell curve (you can see it above), especially if you look at histograms.
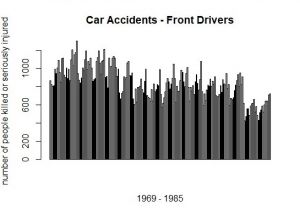
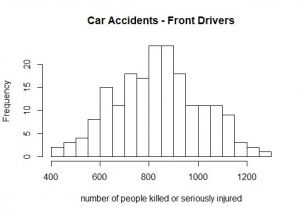
This barplot (at the left) represents the number of front-seat passengers that were killed or seriously injured annually from 1969 to 1985 in the UK. And here comes the magic trick: If you sort the annually number of people from the lowest to the highest (and slightly lower the resolution), a normal distribution evolves (histogram at the left).
If you would like to know, how one can create the diagrams, which you see here, in R, we uploaded the code right below:
# If you want some general information about the "Seatbelt" dataset, at which we will have look, you can use the ?-function.
# As "Seatbelts" is a dataset in R, you can receive a lot of information here.
?Seatbelts
## hint: If you want to see all the datasets, that are available in R, just type:
data()
# to have a look a the dataset "Seatbelts" you can use several commands
## str() to know what data type "Seatbelts" is (e.g. a Time-Series, a matrix, a dataframe...)
str(Seatbelts)
## use show () or just type the name of the dataset ("Seatbelts") to see the table and all data it's containing
show(Seatbelts)
### or
Seatbelts
## summary() to have the most crucial information for each variable: minimum/maximum value, median, mean...
summary(Seatbelts)
# As you saw when you used the str() function, "Seatbelts" is a Time-Series, which is not entirely bad per se,
# but makes it hard to work with it. Like that it is useful to change it into a dataframe (as.data.frame()).
# And simultaneously, we should assign the new dataframe "Seatbelts" to a variable, that we don't lose it and
# can work further with Seatbelts as a dataframe.
seat<-as.data.frame(Seatbelts)
# To choose a single variable of the dataset, we use the '$' operator. If we want a barplot with all front drivers,
# who were killed or seriously injured:
barplot(seat$front)
# For a histogram:
hist(seat$front)
## To change the resolution of the histogram, you can use the "breaks"-argument of the hist-command, which states
## in how many increments the plot should be divided
hist(seat$front, breaks = 30)
hist(seat$front, breaks = 100)
# For a boxplot:
boxplot(seat$front)
Non-normal distributions
Sometimes the world is not normally distributed. At a closer examination, this makes perfect sense under the specific circumstances. It is therefore necessary to understand which reasons exists why data is not normally distributed.
The Poisson distribution
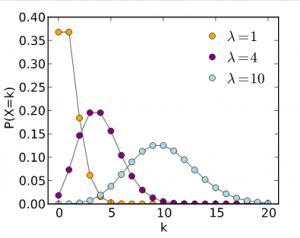
Things that can be counted are often not normally distributed, but are instead skewed to the left. While this may seem curious, it actually makes a lot of sense. Take an example that coffee-drinkers may like. How many people do you think drink one or two cups of coffee per day? Quite many, I guess. How many drink 3-4 cups? Fewer people, I would say. Now how many drink 10 cups? Only a few, I hope. A similar and maybe more healthy example could be found in sports activities. How many people make 30 minute of sport per day? Quite many, maybe. But how many make 5 hours? Only some very few. In phenomenon that can be counted, such as sports activities in minutes per day, most people will tend to a lower amount of minutes, and few to a high amount of minutes. Now here comes the funny surprise. Transform the data following a Poisson distribution, and it will typically follow the normal distribution if you use the decadic logarithm (log). Hence skewed data can be often transformed to match the normal distribution. While many people refrain from this, it actually may make sense in such examples as island biogeography. Discovered by MacArtur & Wilson, it is a prominent example of how the log of the numbers of species and the log of island size are closely related. While this is one of the fundamental basic of ecology, a statistician would have preferred the use of the Poisson distribution.
Example for a log transformation
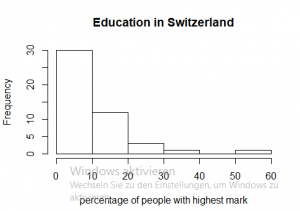
One example for skewed data can be found in the R data set “swiss”, it contains data about socio-economic indicators of about 50 provinces in Switzerland in 1888. The variable we would like to look at is “Examination”, which shows how many men (in %) achieved the highest mark in an army examination. As best grades are mostly a rare phenomenon, it is not surprising that in the majority of provinces only a small percentage of people get the highest mark. As you can see when you look at the first diagram, in 30 provinces only 10 percent of the people achieved the highest mark.
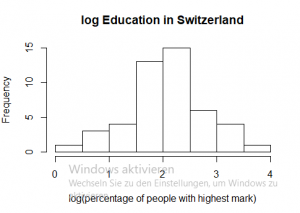
To obtain a normal distribution (which is useful for many statistical tests), we can use the decadic logarithm.
If you would like to know, how to conduct an analysis like on the left-hand side, we uploaded the code right below:
# to get further information about the data set, you can type
?swiss
# to obtain a histogram of the variable Examination
hist(swiss$Examination)
# to transform the data series with the decadic logarith, just use log()
# besides it is good idea to assign the new value to a variable
log_exa<-log(swiss$Examination)
hist(log_exa)
# to make sure, that the data is normally distributed, you can use the shapiro wilk test
shapiro.test(log_exa)
# and as the p-value is higher than 0.05, log_exa is normally distributed
The Pareto distribution
Do you know that most people wear 20 % of their clothes 80 % of their time? This observation can be described by the Pareto distribution. For many phenomena that describe proportion within a given population, you often find that few make a lot, and many make few things. Unfortunately this is often the case for workloads, and we shall hope to change this. For such proportions the Pareto distribution is quite relevant. Consequently, it is rooted in income statistics. Many people have a small to average income, and few people have a large income. This makes this distribution so important for economics, and also for sustainability science.
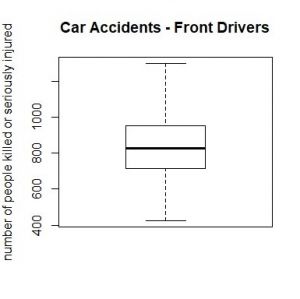
Boxplots
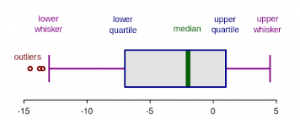
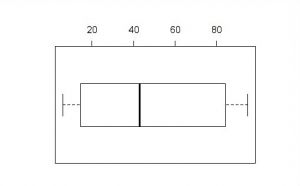
A nice way to visualize a data set is to draw a boxplot. You get a rough overview, how the data is distributed and moreover you can say at a glance if it’s normally distributed. But what are the components of a boxplot and what do they represent?
The median marks the exact middle of your data, which is something different than the mean. If you imagine a series of random numbers, e.g. 3, 5, 7, 12, 26, 34, 40, the median would be 12. But what if your data series comprises an even number of numbers, like 1, 6, 19, 25, 26, 55? You take the mean of the numbers in the middle, which is 22 and hence 22 is your median.
The box of the boxplot is divided in the lower and the upper quartile. In each quarter there are, obviously, a quarter of the data points. To define them, you split the data set in two halves (outgoing from the median) and calculate again the median of each half. In a random series of numbers (6, 7, 14, 15, 21, 43, 76, 81, 87, 89, 95) your median is 43, your lower quartile is 14 and your upper quartile 87.
The space between the lower quartile line and the upper quartile line (the box) is called the interquartile range (IQR), which is important to define the length of the whiskers. The data points which are not in the range of the whiskers are called outliers, which could e.g. be a hint that they are due to measuring errors. To define the end of the upper whisker, you take the value of the upper quartile and add the product of 1,5 * IQR.
Sticking to our previous example: The IQR is the range between the lower (14) and the upper quartile (87), therefore 73. Multiply 73 by 1,5 and add it to the value of the upper quartile: 87 + 109,5 = 196,5
For the lower whisker, the procedure is nearly the same. Again, you use the product of 1,5*IQR, but this time you subtract this value from the lower quartile: Here is your lower whisker: 14 – 109,5 = -95,5 And as there are no values outside of the range of our whiskers, we have no outliers. Furthermore, the whiskers to not extend to their extremes, which we calculated above, but instead mark the most extreme data points.
#boxplot
#our random series of numbers 6, 7, 14, 15, 21, 43, 76, 81, 87, 89, 95
boxplot.example<-c(6,7,14,15,21,43,76,81,87,89,95)
summary(boxplot.example)
# minimum = 6
# maximum = 95
# mean = 48.55
# median = 43
# 1Q = 14.5
# 3Q = 84
# with this information we can calculate the interquartile range
IQR(boxplot.example)
# IQR = 69.5
#lastly we can visualize our boxplot using this comment
boxplot(boxplot.example)
A matter of probability
Probability indicates the likeliness whether something will occur or not. Typically, probabilities are represented by a number between zero and one, where one indicates the hundred percent probability that an event may occur, while zero indicates an impossibility of this event to occur.
The concept of probability goes way back to Arabian mathematicians and was initially strongly associated with cryptography. With rising recognition of preconditions that need to be met in order to discuss probability, concepts such as evidence, validity, and transferability were associated with probabilistic thinking. Probability plays also a role when it came to games, most importantly rolling dice. With the rise of the Enlightenment many mathematical underpinnings of probability were explored, most notably by the mathematician Jacob Bernoulli. Gauss presented a real breakthrough, due to the discovery of the normal distribution, which allowed the feasible approach to link sample size of observations with an understanding of the likelihood how plausible these observations were. Again building on Sir Francis Bacon, the theory of probability reached its final breakthrough once it was applied in statistical hypothesis testing. It is important to notice that this would throw modern statistics into an understanding through the lens of so-called frequentist statistics. This line of thinking dominates up until today, and is widely built on repeated samples to understand the distribution of probabilities across a phenomenon.
Centuries ago Thomas Bayes proposed a dramatically different approach, where however an imperfect or a small sample would serve as basis for statistical interference. Very crudely defined, the two approaches start at exact opposite ends. While frequency statistics demand preconditions such as sample size and a normal distribution for specific statistical tests, Bayesian statistics build on the existing sample size; all calculations base on what is already there. Experts may excuse my dramatic simplification, but one could say that frequentist statistics are top-down thinking, while Bayesian statistics work bottom-up. The history of modern science is widely built on frequentist statistics, which includes such approaches as methodological design, sampling density and replicates, and diverse statistical tests. It is nothing short of a miracle that Bayes proposed the theoretical foundation for the theory named after him more than 250 years ago. Only with the rise of modern computers was this theory explored deeply, and builds the foundation of branches in data science and machine learning. The two approaches are also often coined as objectivists for frequentist probability fellows, and subjectivists for folllowers of Bayes theorem.
Another perspective on the two approaches can be built around the question whether we design studies or whether we base our analysis on the data we just have. This debate is the basis for the deeply entrenched conflicts you have in statistics up until today, and was already the basis for the conflicts between Pearson and Fisher. From an epistemological perspective, this can be associated with the question of inductive or deductive reasoning, although not many statisticians might not be too keen to explore this relation. While probability today can be seen as one of the core foundations of statistical testing, probability as such is increasingly criticised. It would exceed this chapter to discuss this in depth, but let me just highlight that without understanding probability, much of the scientific literature building on quantitative methods is hard to understand. What is important to notice, is that probability has trouble considering Occam's razor. This is related to the fact that probability can deal well with the chance likeliness of an event to a occur, but it widely ignores the complexity that can influence such a likeliness. Modern statistics explore this thought further but let us just realise here: without learning probability we would have trouble reading the contemporary scientific literature.
The probability can be best explained with the normal distribution. The normal distribution basically tells us through probability how a certain value will add to an array of values. Take the example of the height of people, or more specifically people who define themselves as males. Within a given population or country, these have an average height. This means in other words, that you have the highest chance to have this height when you are part of this population. You have a slightly lower chance to have a slightly smaller or larger height compared to the average height. And you have a very small chance to be much smaller or much taller compared to the average. In other words, your probability is small to be very tall or very small. Hence the distribution of height follows a normal distribution, and this normal distribution can be broken down into probabilities. In addition, such a distribution can have a variance, and these variances can be compared to other variances by using a so called f test. Take the example of height of people who define themselves as males. Now take the people who define themselves as females from the same population and compare just these two groups. You may realise that in most larger populations these two are comparable. This is quite relevant when you want to compare the income distribution between different countries. Many countries have different average incomes, but the distribution acroos the average as well as the very poor and the filthy rich can still be compared. In order to do this, the f-test is quite helpful.
External links
Videos
Data Distribution: A crash course
The normal distribution: An explanation
Skewness: A quick explanation
The Poisson distribution: A mathematical explanation
The Pareto Distribution: Some real life examples
The Boxplot: A quick example
Probability: An Introduction
Bayes theorem: A detailed explanation
F test: An example calculation
Articles
Probability Distributions: 6 common distributions you should know
Distributions: A list of Statistical Distributions
Normal Distribution: The History
The Normal Distribution: Detailed Explanation
The Normal Distributions: Real Life Examples
The Normal Distribution: A word on sample size
The weight of nations: How body weight is distributed across the world
Non normal distributions: A list
Reasons for non normal distributions: An explanation
Different distributions: An overview by Aswath Damodaran, S.61
The Poisson Distribution: The history
The Poisson Process: A very detailed explanation with real life examples
The Pareto Distribution: An explanation
The pareto principle and wealth inequality: An example from the US
History of Probability: An Overview
Frequentist vs. Bayesian Approaches in Statistics: A comparison
Bayesian Statistics: An example from the wizarding world
Probability and the Normal Distribution: A detailed presentation
Compare your income: A tool by the OECD
F test: An example in R