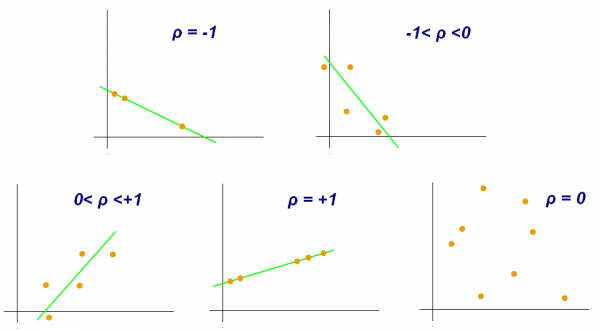Causality and correlation (German)
Note: This is the German version of this entry. The original, English version can be found here: Causality and correlation. This entry was translated using DeepL and only adapted slightly. Any etymological discussions should be based on the English text.
Contents
Korrelative Zusammenhänge
Korrelationen können uns sagen, ob zwei Variablen miteinander in Beziehung stehen. Eine Korrelation sagt uns jedoch nicht, was sie bedeutet. Dies ist wichtig zu beachten, da viele Korrelationen berechnet werden, aber es liegt an uns, diese Beziehungen zu interpretieren.
Es liegt potenziell in unserer normativen Kapazität, Hypothesen abzuleiten, aber es kann auch wirkungsvoll sein, keine Hypothesen abzuleiten und einen rein induktiven Ansatz für eine Korrelation zu haben. Wir leben in einer Welt der großen Datenmengen, und das in zunehmendem Maße. Es gibt eine Fülle von Informationen, und sie wächst buchstäblich von Minute zu Minute. Während die Aufklärung und dann die Moderne eine Welt der Wissenschaft auf der Grundlage der Macht der Hypothese aufbauten, war diese Wissenschaft auch begrenzt. Wir wissen heute, dass der mächtige Schritt, eine Hypothese aufzustellen, nur einen Teil des Bildes bietet, und mächtige Erfindungen und Fortschritte kamen durch Induktion. Viele Fortschritte in der Wissenschaft beruhten auf induktiven Ansätze. Man denke nur an Antibiotika, deren Entdeckung ein reiner Zufall war.
Mit der Vorhersagekraft von Korrelationen und dem Aufstieg des maschinellen Lernens und den damit verbundenen, viel komplexeren Ansätzen brach eine neue Welt an. Heute basieren Vorhersagen auf einfachen Korrelationen und der Erkennung von Leistungsmustern in der Fülle der Daten, mit denen wir konfrontiert sind. Obwohl ein Großteil der eigentlichen Mathematik sehr viel komplizierter ist, sind Vorschläge prominenter Online-Shops zu dem, was Sie vielleicht als nächstes kaufen möchten - im Prinzip - ausgefeilte Ausarbeitungen von Korrelationen. Wir verstehen nicht, warum bestimmte Leute, die eine Sache kaufen, auch eine andere Sache kaufen, aber das Aufzeigen dieser Beziehung erhöht den Umsatz. Natürlich ist die Welt komplizierter, und wieder einmal können diese Modelle glücklicherweise nicht alles erklären. Ich weiß selbst, dass ich vor der totalen Vorhersage der Maschinen sicher bin, solange mein Musikdienst mir vorschlägt, Oasis - die schlimmste Beleidigung für mich - zu hören. Dennoch, mit der Vorhersagekraft kommt einmal mehr eine große Verantwortung, und wir werden sehen, wie Korrelationen und ihre Vorhersagekraft es uns ermöglichen werden, mehr Theorien auf der Grundlage unserer induktiven Perspektive auf Daten abzuleiten. Durch die Digitalisierung der Daten ist viel zu lernen, aber es liegt immer noch an uns, die Korrelationen zu interpretieren. Es wird sehr schwer sein, dies einer Maschine beizubringen, daher liegt es in unserer Verantwortung, die Datenanalyse durch Schlussfolgerungen zu interpretieren.
Der Aufstieg der Korrelationen
Angetrieben durch die allgemeine Entwicklung der Wissenschaft während der Aufklärung begannen sich die Zahlen anzuhäufen. Die zunehmenden technologischen Möglichkeiten, immer mehr Informationen zu messen, speichern diese Informationen nur langsam, und die Menschen begannen sich zu fragen, ob diese Zahlen zu etwas führen könnten. Die wachsenden Zahlen hatten unterschiedliche Quellen, einige stammten aus der Wissenschaft, wie der Astronomie oder anderen Zweigen der Naturwissenschaften. Andere prominente Zahlenquellen stammten aus dem Ingenieurwesen, und sogar andere aus der Wirtschaft, zum Beispiel durch die doppelte Buchhaltung. Dank der gemeinsamen Anstrengungen von Adrien-Marie Legendre und Carl Friedrich Gauß bot die Mathematik den ersten Ansatz, eine Datenzeile mit einer anderen in Beziehung zu setzen - die Methode der kleinsten Quadrate.
Wie hängt eine kontinuierliche Variable mit einer anderen zusammen? Die Büchse der Pandora wurde geöffnet, und es tauchten Fragen auf. Ökonomen waren die ersten, die die Regressionsanalyse in größerem Maßstab einsetzten, indem sie alle möglichen wirtschaftlichen und sozialen Indikatoren miteinander in Beziehung setzten und so ein immer komplexeres Controlling, Management und vielleicht sogar Verständnis für statistische Zusammenhänge aufbauten. Das Bruttoinlandsprodukt (BIP) wurde für einige Zeit zu einer Art Lieblings-Spielzeug für viele Ökonomen, und Wachstum wurde zu einem Kernziel vieler Analysen, um die Politik zu informieren. Was die Leute im Grunde taten, war die Frage, wie eine Variable mit einer anderen Variable zusammenhängt.
Erhöht eine gute Ernährung die Lebenserwartung?
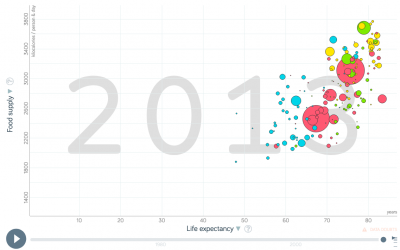
Hängt eine höhere Lebenserwartung mit der landwirtschaftlichen Fläche eines Landes zusammen?
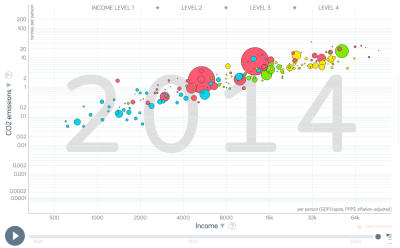
Korreliert ein höheres Einkommen mit höheren CO2-Emissionen?
Wichtige Elemente von Korrelationen
Es gibt einige zentrale Fragen im Zusammenhang mit der Anwendung und dem Lesen von Korrelationen. Diese können immer dann von Interesse sein, wenn man den Korrelationskoeffizienten zur Hand hat - zum Beispiel in einer Statistiksoftware - oder wenn man ein Korrelationsdiagramm sieht.
1) Ist die Beziehung zwischen zwei Variablen positiv oder negativ? Wenn eine Variable zunimmt und die andere ebenfalls zunimmt, haben wir eine positive ("+") Korrelation. Dies trifft auch zu, wenn beide Variablen abnehmen. Zum Beispiel führt eine größere Körpergröße zu einem signifikanten Anstieg des Körpergewichts. Wenn hingegen eine Variable zunimmt und die andere abnimmt, ist die Korrelation negativ ("-"): Zum Beispiel ist die Beziehung zwischen "Pizza gegessen" und "Pizza übrig" negativ. Je mehr Pizzastücke gegessen werden, desto weniger Stücke sind noch da. Diese Richtung der Beziehung sagt viel darüber aus, wie zwei Variablen logisch miteinander verbunden sein könnten. Der normative Wert einer positiven oder negativen Beziehung hat in der Regel starke Implikationen, insbesondere wenn beide Richtungen theoretisch möglich sind. Deshalb ist es wichtig, die Richtung einer korrelativen Beziehung interpretieren zu können.
2) Ist der Korrelationskoeffizient klein oder groß? Der Korrelationskoeffizient kann zwischen -1 und +1 liegen und ist ein wichtiges Maß für die Bewertung der Stärke einer statistischen Beziehung. Datenpunkte können in einem scatter plot stark streuen oder es kann eine eher lineare Beziehung bestehen - und alles dazwischen. Ein Beispiel für eine perfekte positive Korrelation (mit einem Korrelationskoeffizienten r von +1) ist die Beziehung zwischen der Temperatur in Celsius und Fahrenheit. Dies sollte nicht überraschen, da Fahrenheit als 32 + 1,8° C definiert ist. Daher ist ihre Beziehung vollkommen linear, was zu einem so starken Korrelationskoeffizienten führt. Wir können also sagen, dass 100 % der Temperaturschwankungen in Fahrenheit durch die Temperatur in Celsius erklärt werden.
Andererseits kann es vorkommen, dass die Daten zweier Variablen in einem Streudiagramm weit verstreut sind und kein signifikanter Zusammenhang festgestellt werden kann. Der Korrelationskoeffizient r liegt dann vielleicht bei 0,1 oder 0,2. In diesem Fall kann man davon ausgehen, dass keine starke Beziehung zwischen den beiden Variablen besteht und dass die eine Variable die andere nicht erklärt.
Je höher der Korrelationskoeffizient einer Beziehung ist, desto mehr Bedeutung haben diese Beziehungen, so könnte man argumentieren. Wenn die Punkte wie Sterne am Himmel verteilt sind, dann ist die Beziehung wahrscheinlich nicht signifikant und interessant. Natürlich ist dies nicht ganz verallgemeinerbar, aber es stimmt auf jeden Fall, dass eine neutrale Beziehung nur aussagt, dass die Beziehung keine Bedeutung hat. Gleichzeitig können auch schwächere Beziehungen wichtige erste Einblicke in die Daten geben, und wenn zwei Variablen irgendeine Art von Beziehung aufweisen, ist es gut, die Stärke zu kennen. Wenn man übt, die Stärke einer Korrelation schnell zu erfassen, wird man sehr schnell in der Lage sein, Beziehungen in Daten zu verstehen. Diese Fähigkeit ist für jeden wichtig, der sich für die Annäherung von Fakten durch quantitative Daten interessiert.
3) Was erklärt die Beziehung zwischen zwei Variablen? Dies ist bereits eine fortgeschrittene Fähigkeit, die eher mit der Regressionsanalyse zusammenhängt. Wenn Sie also die Stärke einer Korrelation und ihre Richtung untersucht haben, sind Sie im Allgemeinen gut gerüstet. Aber manchmal ändern sich diese Maße in verschiedenen Teilen der Daten.
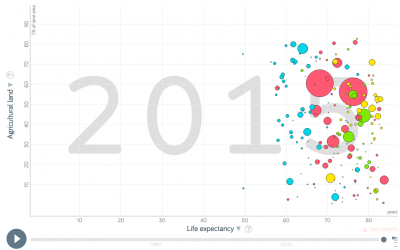
Um dies zu veranschaulichen, betrachten wir das Beispiel des prozentualen Anteils der in der Landwirtschaft arbeitenden Menschen in den einzelnen Ländern. Weltweit gibt es bei Menschen mit niedrigem Einkommen (<5000 Dollar/Jahr) eine große Variabilität in Bezug auf die Beschäftigung in der Landwirtschaft: die Hälfte der Bevölkerung des Tschad arbeitet in der Landwirtschaft, während es in Simbabwe nur 10 % sind. Bei einem Einkommen von mehr als 15.000 Dollar/Jahr gibt es jedoch kaum Schwankungen beim Prozentsatz der Menschen, die in der Landwirtschaft arbeiten: er ist immer sehr niedrig. Würde man dies grafisch darstellen, so würde man sehen, dass die Datenpunkte in den unteren x-Werten (mit x als Einkommen) eher breit gestreut sind, in den höheren Einkommensbereichen (= x-Werte) jedoch linearer verteilt sind. Dies hat Gründe, und es gibt wahrscheinlich eine oder mehrere Variablen, die diese Variabilität erklären. Vielleicht gibt es andere Faktoren, die einen stärkeren Einfluss auf den Anteil der Landwirte in den unteren Einkommensgruppen haben als in den höheren Einkommensgruppen, wo das Einkommen ein guter Prädiktor ist.
Eine Korrelationsanalyse hilft uns, solche Schwankungen in der Datenbeziehung zu erkennen, und wir sollten die Korrelationskoeffizienten und die Richtung der Beziehung für verschiedene Teile der Daten betrachten. Oft gibt es eine stärkere Beziehung in Teilen des Datensatzes und eine schwächere Beziehung in anderen Teilen des Datensatzes. Diese Unterschiede sind wichtig, da sie auf zugrunde liegende Einflussvariablen oder Faktoren hindeuten, die wir noch nicht verstanden haben.
Kausalität
Wie soll man hier Anfang und Ende finden?
Kausalität ist eines der am meisten missbrauchten und missverstandenen Konzepte in der Statistik. Dabei ist es der Kern der Tatsache, dass alle Statistiken normativen Charakter haben. Während viele Dinge kausal miteinander verbunden sein können, sind es viele nicht. Das Problem besteht darin, dass wir uns wünschen, dass bestimmte Dinge kausal miteinander verbunden sind, während wir wollen, dass andere Dinge nicht kausal miteinander verbunden sind. Diese Verwirrung hat viele Wurzeln und erstreckt sich über so unbändige Bereiche wie Glauben, Psychologie, Kultur, soziale Konstrukte und so weiter. Kausalität kann alles sein, was an der Statistik gut ist, und sie kann ebenso alles sein, was an der Statistik falsch ist. Mit anderen Worten: Sie kann alles sein, was an uns Menschen gut ist, aber sie kann auch die Ursache für alles sein, was bei uns falsch ist.
Was ist attraktiv an der Kausalität? Die Menschen suchen nach Erklärungen, und diese ständige Suche ist wahrscheinlich einer der Bausteine unserer Zivilisation. Die Menschen suchen nach Gründen, um Phänomene und Muster zu erklären, oft mit dem Ziel der Vorhersage. Wenn ich einen Kausalzusammenhang verstanden habe, kann ich vielleicht mehr über die Zukunft wissen und davon profitieren, entweder auf diese Zukunft vorbereitet zu sein oder zumindest richtig reagieren zu können.
Das Problem mit der Kausalität besteht darin, dass sowohl verschiedene Wissenschaftszweige als auch verschiedene philosophische Strömungen unterschiedliche Erklärungen für Kausalität haben, und es gibt eine aufregende Vielfalt von Theorien über Kausalität. Lassen Sie uns das Thema systematisch angehen.
Die high road und die low road of causality
Nehmen wir den ersten Extremfall: die Theorie, dass Störche die Babys bringen. Offensichtlich ist dies nicht wahr. Einen kausalen Zusammenhang zwischen diesen beiden herzustellen, ist offensichtlich ein Fehler. Nehmen wir nun den anderen Extremfall: Sie fallen eine Treppe hinunter und brechen sich beim Sturz das Bein. Es besteht offensichtlich eine Form des Kausalzusammenhangs zwischen diesen beiden Handlungen, nämlich dass Sie sich beim Sturz die Treppe das Bein gebrochen haben. Dies erfordert jedoch bereits ein gewisses Maß an Abstraktion, einschließlich der Annahme, dass Sie es waren, der die Treppe hinuntergefallen ist, dass Sie Ihr Bein verdreht oder mit genügend Kraft auf eine Treppe geschlagen haben, dass Sie nicht zu schwach waren, um dem Aufprall standzuhalten usw. Es gibt also eine sehr detaillierte Kette von Ereignissen, die sich abspielt, wenn Sie anfangen, das Gleichgewicht zu verlieren, und sich das Bein brechen. Unser Verstand vereinfacht dies in "weil ich die Treppe hinuntergefallen bin, habe ich mir das Bein gebrochen". Natürlich geben wir weder der Person, die die Treppe gebaut hat, noch unseren Eltern die Schuld dafür, dass sie uns in diese Welt gebracht haben, wo wir uns dann das Bein gebrochen haben. Diese Dinge stehen nicht in kausalem Zusammenhang.
Aber stellen Sie sich nun vor, dass der Bauarbeiter die Treppe nicht richtig konstruiert hat und dass eine Treppe etwas höher ist als die andere. Wir behaupten nun, dass es die Schuld des Bauarbeiters ist. Wie viel höher muss diese eine Treppe jedoch sein, damit wir nicht uns selbst die Schuld geben, sondern dem Bauarbeiter? Sie haben den Punkt verstanden.
Kausalität ist eine Konstruktion, die sich in unserem Kopf abspielt. Wir schaffen ein abstraktes Weltbild, und in diesem abstrakten Weltbild entwerfen wir eine Version der Wirklichkeit, die vereinfacht genug ist, um beispielsweise zukünftige Ereignisse zu erklären, aber es ist nicht zu einfach, da wir damit nichts Bestimmtes oder kleinere Gruppen von Ereignissen erklären könnten.
Kausalität ist also eine Abstraktion, die auf Occam's Razor folgt, schlage ich vor. Und da wir alle unsere eigene Version von Ockhams Rasiermesser im Kopf haben, sind wir oft anderer Meinung, wenn es um Kausalität geht. Ich glaube, das hängt nur damit zusammen, dass sich bei der Analyse alles auflöst. Wenn wir irgendeinen Zusammenhang zwischen Ereignissen analysieren, dann kann sich auch der kausale Zusammenhang auflösen oder irrelevant werden. Letztendlich ist die Kausalität eine Wahl.
Nehmen wir das Beispiel von medizinischen Studien, wo die meisten Studien auf einem korrelativen Design aufbauen und testen, wie zum Beispiel die Einnahme von Ibuprofen gegen Erkältung helfen kann. Wenn ich Kopfschmerzen habe und Ibuprofen einnehme, kann es mir in den meisten Fällen helfen. Aber verstehe ich, wie es mir hilft? Ich verstehe vielleicht einige Teile davon, aber auf zellulärer Ebene verstehe ich es nicht wirklich. Es gibt wieder eine gewisse Abstraktionsebene.
Was jetzt für die Kausalität am relevantesten ist, ist die bloße Tatsache, dass eine Sache durch eine andere Sache erklärt werden kann. Wir müssen nicht alles in allen Einzelheiten verstehen, und ich habe oben bereits gesagt, dass dies letztlich sehr schwer für uns wäre. Stattdessen müssen wir verstehen, ob das Wegnehmen der einen Sache verhindert, dass die andere Sache geschieht. Wenn ich nicht die Treppe hinuntergegangen wäre, hätte ich mir nicht das Bein gebrochen.
Seit Aristoteles und seiner Frage "Was ist seine Natur?" nervt uns die Knappheit der wahren Kausalität oder tiefen Kausalität. Ich schlage vor, dass es eine high road of causality und eine low road of causality gibt. Die high road ermöglicht es uns, alles darüber zu erklären, wie zwei Dinge oder Phänomene miteinander verbunden sind. Obwohl ich dies ablehne, halten ihn viele Denkschulen für sehr relevant. Ich für meinen Teil bevorzuge die low road: Ist eine Sache oder ein Phänomen kausal mit einer anderen Sache oder einem anderen Phänomen verbunden; wenn ich das eine wegnehme, wird das andere nicht geschehen. Das bedeutet automatisch, dass ich Kompromisse eingehen muss, wie viel ich von der Welt verstehe.
Ich schlage vor, dass wir nicht alles verstehen müssen. Unsere Vorfahren haben nicht wirklich verstanden, warum es in einem Gebiet mit vielen Raubtieren zum Tod führen kann, wenn man im Dunkeln ohne Fackel und Waffe - oder besser noch in einer größeren Gruppe - hinausgeht. Es genügte ihnen, zu wissen, dass sie in der Nacht in Sicherheit sein würden. Das genügt mir auch.
Einfache und komplexe Kausalität
Versuchen wir, die kausalen Zusammenhänge Schritt für Schritt zu verstehen. Zu diesem Zweck können wir kurz zwei Arten von kausalen Beziehungen unterscheiden.
Statistische Korrelationen implizieren Kausalität, wenn eine Variable (A) aktiv durch eine Variable (B) getrieben wird. Wenn B weggenommen oder verändert wird, verändert sich auch A oder wird nicht mehr vorhanden. Diese Beziehung gehört zu den am häufigsten bekannten Beziehungen in der Statistik, aber sie hat gewisse Probleme. In erster Linie können zwei Variablen kausal miteinander verbunden sein, aber die Beziehung kann schwach sein. Zink kann sicherlich gegen die Erkältung helfen, aber es ist nicht garantiert, dass Zink uns heilen wird. Es ist eine schwache kausale Korrelation.
Zweitens kann eine kausale Beziehung der Variablen A und B mit einer Variablen C und weiteren Variablen D, E, F usw. interagieren. In diesem Fall sprechen viele Menschen von komplexen Beziehungen. Komplexe Beziehungen können kausal sein, aber sie sind dennoch komplex, und diese Komplexität kann Menschen verwirren. Schließlich können statistische Beziehungen durch Bias, Beschränkungen der Stichprobengröße und viele andere Herausforderungen, mit denen die Statistik konfrontiert ist, beeinflusst werden. Diese Herausforderungen sind bekannt, zunehmend untersucht, aber oft nicht lösbar.
Struktur ins Chaos bringen: Normativität und Plausibilität
Ausgehend von dem Gedanken, dass unser Verstand umherwandert, um kausale Zusammenhänge zu finden, und dann mit Experimenten und Hypothesen als mächtige Werkzeuge, begannen Wissenschaftler damit, Theorien abzuleiten und zu revidieren, die auf Versuchsanordnungen basierten. Manchmal war es auch umgekehrt, da viele Theorien erst später durch Beobachtung oder wissenschaftliche Experimente bewiesen wurden. Nachdem die Kausalität durch wissenschaftliche Theorien erklärt worden war, entstand eine Kombination, die unter vielen anderen Dingen zu physikalischen Gesetzen, gesellschaftlichen Paradigmen und psychologischen Modellen führte.
Die Plausibilität begann ihre Herrschaft als ein Schlüsselkriterium der modernen Wissenschaft. Plausibilität bedeutet grundsätzlich, dass Beziehungen nur dann kausal sein können, wenn die Beziehungen nicht nur wahrscheinlich, sondern auch vernünftig sind. Um die Wahrscheinlichkeit kümmert sich die Statistik. Aber es ist der menschliche Verstand, der die Vernunft aus den Daten ableitet, was die Kausalität zu einem zutiefst normativen Akt macht. Kontrafaktische Theorien können später unsere Kausalität widerlegen, weshalb wir keine absolute Wahrheit kennen können, aber wir können uns ihr annähern. Unsere Annahmen können auch später noch falsifiziert werden.
So weit, so gut. Es ist erwähnenswert, dass Aristoteles einige interessante metaphysische Ansätze zur Kausalität hatte, ebenso wie Buddhisten und Hindus. Wir werden diese hier der Einfachheit halber ignorieren.
Hume's Kriterien für Kausalität
Es scheint offensichtlich, aber eine notwendige Bedingung für Kausalität ist die zeitliche Ordnung (Neumann 2014, S.74-78). Zeitliche Kausalketten können als Beziehungen definiert werden, in denen eine Wirkung eine Ursache hat. Ein Ereignis A kann direkt auf eine Handlung B folgen. Mit anderen Worten, A wird durch B verursacht. Wir denken oft, dass wir solche Kausalbeziehungen in einer zeitlichen Kette verwurzelt sehen. Die komplexe Debatte über Impfungen und Autismus kann als ein solches Beispiel angesehen werden. Die Impfgegner sind der Meinung, dass der Autismus durch Impfungen verursacht wurde, während Mediziner argumentieren, dass der Ausbruch von Autismus lediglich zur gleichen Zeit stattfand, wie die Impfungen als Teil des notwendigen Schutzes unserer Gesellschaft vorgenommen werden. Der zeitliche Zusammenhang wird in diesem Fall als reiner Zufall angesehen. Viele solcher zeitlichen Beziehungen werden daher angenommen, aber unser Verstand täuscht uns oft, da wir uns täuschen lassen wollen. Wir wollen Ordnung im Chaos, und für viele Menschen ist Kausalität Glückseligkeit. Die Geschichte versucht oft, Kausalitäten zu finden, doch wie einst behauptet wurde, wird die Geschichte von den Siegreichen geschrieben, d.h. sie ist subjektiv. Ein Modell zu haben, das die eigene Realität erklärt - danach suchen viele heute, und eine Art zeitliche Kausalkette zu haben, scheint eine der Sehnsüchte vieler Menschen zu sein. Wissenschaftliche Experimente wurden erfunden, um solche Kausalitäten zu testen, und die menschliche Gesellschaft entwickelte sich. Heute scheint es nahezu unmöglich zu sein, nichts über die Schwerkraft zu wissen - in gewissem Sinne wissen wir das alle, ja - aber die ersten physikalischen Experimente haben uns geholfen, dies zu beweisen. So half uns das wissenschaftliche Experiment, die zeitliche Kausalität zu erforschen, und medizinische Studien können als eine der am stärksten vorangetriebenen Fortsetzungen davon angesehen werden.
Wir können jedoch auf Hume aufbauen, der in seiner Abhandlung über die menschliche Natur die drei unten erwähnten Kriterien benannte. Um seine Worte zu paraphrasieren: Die Kausalität ist in Raum und Zeit zusammenhängend, die Ursache liegt vor der Wirkung, und es besteht eine ständige Verbindung zwischen Ursache und Wirkung. Es lohnt sich, auch die anderen von ihm erwähnten Kriterien zu betrachten.
1. Hume behauptet, dass die gleiche Ursache immer die gleiche Wirkung hervorruft. In der Statistik weist dies auf das Kriterium der Reproduzierbarkeit hin, das eines der Rückgrate des wissenschaftlichen Experiments ist. Dies mag in Zeiten von Einzelfallstudien als schwierig angesehen werden, unterstreicht aber gleichzeitig, dass der Wert solcher Studien eindeutig relevant, aber nach diesem Kriterium begrenzt ist.
2. Wenn mehrere Objekte denselben Effekt hervorrufen, muss es darüber hinaus ein verbindendes Kriterium unter ihnen geben, das den Effekt verursacht. Ein gutes Beispiel dafür sind Gewichte auf einer Waage. Mehrere Gewichte können addiert werden, um die gleiche - gegenläufige - Wirkung zu erzielen. Man müsste eine hohe Anzahl von Federn stapeln, um die gleiche Wirkung zu erzielen wie, sagen wir, 50 kg Gewicht (und es wäre bedauerlich für die Vögel). Auch dies ist für die moderne Wissenschaft von großer Bedeutung, da die Suche nach einheitlichen Kriterien bei den Datenmengen, die wir heutzutage oft analysieren, ein Schlüsselziel ist.
3. Wenn zwei Objekte eine unterschiedliche Wirkung haben, muss es einen Grund geben, der den Unterschied erklärt. Diese dritte Annahme von Hume ist eine direkte Konsequenz aus der zweiten. Was Faktoren vereint, kann wichtig sein, aber ebenso wichtig kann sein, was Faktoren unterscheidet. Dies ist oft der Grund, warum wir glauben, dass es einen kausalen Zusammenhang zwischen zwei Dingen gibt, obwohl es eindeutig keinen gibt. Stellen Sie sich vor, eine böse Person gibt Ihnen koffeinfreien Kaffee, während Sie an Koffein gewöhnt sind. Die Wirkung könnte schwerwiegend sein, und es ist klar, dass das Koffein in dem Kaffee, der Sie aufweckt, diesen Kaffee von dem entkoffeinierten Kaffee unterscheidet.
Zusammenfassend lässt sich sagen, dass die Kausalität ein Chaos in unseren Gehirnen ist. Wir täuschen uns öfter über die Kausalität, als wir denken, unser Gehirn ist fest verdrahtet, Verbindungen zu finden, und lässt sich oft zur Annahme einer Kausalität verleiten.. Gleichermaßen wollen wir oft die Kausalität vernachlässigen, wenn sie eindeutig eine Tatsache ist. Wir irren uns also recht oft. Bleiben Sie im Zweifelsfall bei Hume und den oben genannten Kriterien. Sich bei der Analyse von Korrelationen auf diese zu verlassen, erfordert am Ende des Tages einfach Übung.
The author of this entry is Henrik von Wehrden.