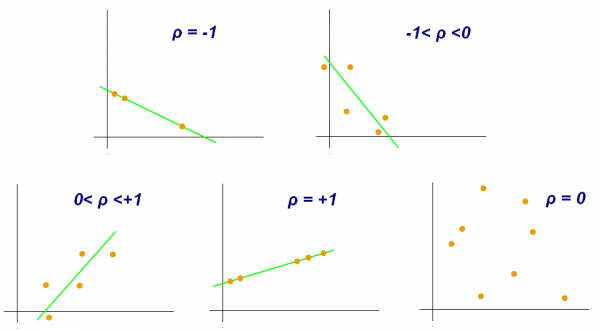Causality and correlation
Note: The German version of this entry can be found here: Causality and correlation (German)
Note: This entry focuses on the connection between correlations and causality. More details on Correlations as a scientific method can be found in this entry: Correlations. More details on Causality in science can be found in the entry on Causality. More on Regressions can be found here: Regression Analysis.
Contents
Correlative relations
Correlations can tell us whether two variables are related. A correlation does not tell us however what this correlation means. This is important to note, as there are many correlations being calculated, but it is up to us to interpret these relations.
It is potentially within our normative capacity to derive hypotheses from a theory (deduction), but it can also be powerful to not derive hypotheses and have a purely inductive approach to a correlation. We live in a world of big data, and increasingly so. There is a wealth of information out there, and it is literally growing by the minute. While the Enlightenment and then the Modernity built a world of science based on the power of hypotheses, this science was also limited. We know today that the powerful step of building a hypothesis offers only a part of the picture, and powerful inventions and progress came from induction. Much progress in science was based on inductive approaches. Consider antibiotics, whose discovery was a mere accident.
With the predictive power of correlations and the rise of of machine learning and the associated, much more complex approaches, a new world dawned upon us. Today, predictions are based on simple correlations and the recognition of powerful patterns in the wealth of data we face. Although much of the actual mathematics are much more complicated, suggestions of prominent online shops on what you may want to buy next are - in principle - sophisticated elaborations of correlations. We do not understand why certain people that buy one thing buy also another thing, but promoting this relation increases sales. Of course the world is more complicated, and once more these models cannot explain everything. As long as my music service suggests me to listen to Oasis - the worst insult to me - we are safe from the total prediction of the machines.
Still, with predictive power once more comes great responsibility, and we shall see how correlations and their predictive power will allow us to derive more theories based on our inductive perspective on data. Much is to be learned through the digitalisation of data, but it is still up to us to interpret correlations. This will be very hard to teach to a machine, hence it is our responsibility to interpret data analysis through reasoning.
The Rise of Correlations
Propelled through the general development of science during the Enlightenment, numbers started piling up. The increasing technological possibilities to measure more and more information are slow to store this information, and people started wondering whether these numbers could lead to something. The increasing numbers had diverse sources, some were from science, such as Astronomy or other branches of natural sciences. Other prominent sources of numbers were from engineering, and even other from economics, such as double bookkeeping. It was thanks to the tandem efforts of Adrien-Marie Legendre and Carl Friedrich Gauss that mathematics offered the first approach to relate one line of data with another - the methods of least squares.
How is one continuous variable related to another? Pandora's box was opened, and questions started to emerge. Economists were the first who utilised regression analysis at a larger scale, relating all sorts of economical and social indicators with each other. A regression implies a causal link between two continuous variables, which makes it different from a correlation, where two variables are related, but not necessarily causally linked. (For more on regressions, please refer to the entry on Regression Analysis). The Gross domestic product (GDP) became for quite some time kind of the favorite toy for many economists, and growth became a core goal of many analyses to inform policy. What people basically did is ask themselves how one variable is related to another variable.
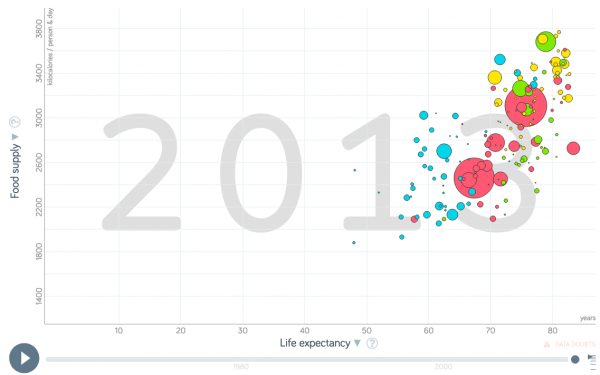
If nutrition of people increases, do they live longer?
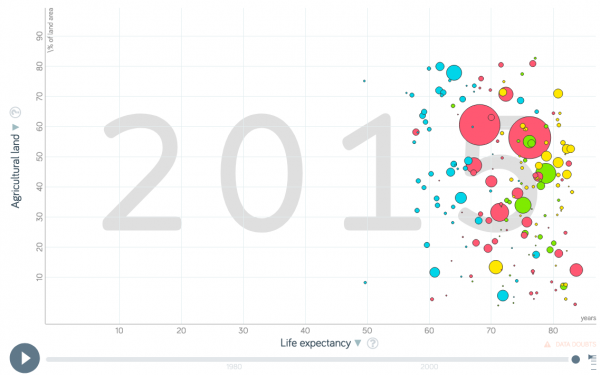
Does a high life expectancy relate to more agricultural land area within a country?
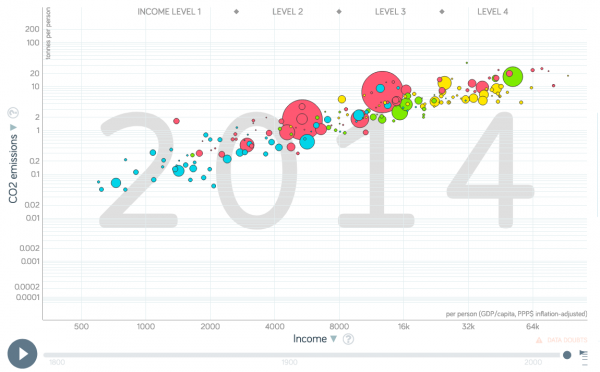
Is a higher income related to more CO2 emissions at a country scale?
Core elements of correlations
There are some core questions related to the application and reading of correlations. These can be of interest whenever you have the correlation coefficient at hand - for example, in a statistical software - or when you see a correlation plot.
1) Is the relationship between two variables positive or negative? If one variable increases, and the other one increases too, we have a positive ("+") correlation. This is also true if both variables decrease. For instance, being taller leads to a significant increase in body weight. On the other hand, if one variable increases, and the other decreases, the correlation is negative ("-"): for example, the relationship between 'pizza eaten' and 'pizza left' is negative. The more pizza slices are eaten, the fewer slices are still there. This direction of the relationship tells you a lot about how two variables might be logically connected. The normative value of a positive or negative relation typically has strong implications, especially if both directions are theoretically possible. Therefore it is vital to be able to interpret the direction of a correlative relationship.
2) Is the correlation coefficient small or large? It can range from -1 to +1, and is an important measure when we evaluate the strength of a statistical relationship. Data points may scatter widely in a scatter plot, or there may be a rather linear relationship - and everything in between. An example for a perfect positive correlation (with a correlation coefficient r of +1) is the relationship between temperature in Celsius and Fahrenheit. This should not be surprising, since Fahrenheit is defined as = C (temperature in °C) x 1.8 + 32. Therefore, their relationship is perfectly linear, which results in such a strong correlation coefficient. We can thus say that 100% of the variation in temperature in Fahrenheit is explained by the temperature in Celsius.
On the other hand, you might encounter data of two variables that is scattered all the way in a scatter plot and you cannot find a significant relationship. The correlation coefficient r might be around 0.1, or 0.2. Here, you can assume that there is no strong relationship between these two variables, and that one variable does not explain the other one.
The stronger the correlation coefficient of a relation is, the more may these relations matter, some may argue. If the points are distributed like stars in the sky, then the relationship is probably not significant and interesting. Of course this is not entirely generalizable, but it is definitely true that a neutral relation only tells you that the relation does not matter. At the same time, even weaker relations may give important initial insights into the data, and if two variables show any kind of relation, it is good to know the strength. By practicing to quickly grasp the strength of a correlation, you become really fast in understanding relationships in data. Having this kind of skill is essential for anyone interested in approximating facts through quantitative data.
3) What does the relationship between two variables explain? This is already an advanced skill, and is rather related to regression analysis. So if you have looked at the strength of a correlation, and its direction, you are good to go generally. But sometimes, these measures change in different parts of the data.
To illustrate this, let us have a look at the example of the percentage of people working in Agriculture within individual countries. Across the world, people at a low income (<5000 Dollar/year) have a high variability in terms of agricultural employment: half of the population of the Chad work in agriculture, while in Zimbabwe it is only 10 %. However, at an income above 15000 Dollar/year, there is hardly any variance in the percentage of people that work in agriculture: it is always very low. If you plotted this, you would see that the data points are rather broadly spread in the lower x-values (with x as the income), but are more linearly spread in the higher income areas (= x values). This has reasons, and there are probably one or several variables that explain this variability. Maybe there are other factors that have a stronger influence on the percentage of farmers in lower income groups than for higher incomes, where the income is a good predictor.
A correlation analysis helps us identify such variances in the data relationship, and we should look at correlation coefficients and the direction of the relationship for different parts of the data. We often have a stronger relation across parts of the dataset, and a weaker relation across other parts of the dataset. These differences are important, as they hint at underlying influencing variables or factors that we did not understand yet.
Causality
Where to start, how to end?
Causality is one of the most misused and misunderstood concepts in statistics. All the while, it is at the heart of the fact that all statistics are normative. While many things can be causally linked, many are not. The problem is that we dearly want certain things to be causally linked, while we want other things not to be causally linked. This question of causality may seem abstract, but it is relvevant every time we ask whether two or more phenomena are causally linked. Does demoacracy drive wealth? Does a student's socio-economic background influence their school grades? Does sustainability reporting decrease the climate emissions of a company?
The confusion about causality and correlation has many roots, and spans across such untameable arenas such as faith, psychology, culture, social constructs and so on. Causality can be everything that is good about statistics, and it can be equally everything that is wrong about statistics. To put it in other words: it can be everything that is great about us humans, but it can be equally the root cause of everything that is wrong with us.
What is attractive about causality? People search for explanations, and this constant search is probably one of the building blocks of our civilisation. Humans look for reasons to explain phenomena and patterns, often with the goal of prediction. If I understood a causal relation, I may be able to know more about the future, cashing in on being either prepared for this future, or at least being able to react properly.
The problem with causality is that different branches of science as well as different streams of philosophy have different explanations of causality, and there exists an exciting diversity of theories about causality. Let us approach the topic systematically.
The high and the low road of causality
Let's take the first extreme case: the theory that storks bring the babies. Obviously this is not true. Creating a causal link between these two is obviously a mistake. Now lets take the other extreme case, you fall down a flight of stairs, and in the fall break your leg. There is obviously some form of causal link between these two actions, that is falling down the stairs caused you to break your leg. However, this already demands a certain level of abstraction, including the acceptance that it was you who lost balance, you who did fall down the stairs, you twisting your leg or hitting a stair with enough force etc. There is, hence, a very detailed chain of events happening between you starting to lose your balance, and you breaking your leg. Our mind simplifies this into “because I fell down the stairs, I broke my leg”. Obviously, we do not blame the person who built the stairs, and we do not blame our parents for bringing us into this world, where we then broke our leg. These things are not causally linked.
But, imagine now that the construction worker did not construct the stairs the proper way, and that one stair is slightly higher than the other stairs. We now claim that it is the fault of the construction worker. However, how much higher does this one stair need to be so that we blame not ourselves, but the construction worker? You get the point.
Causality is a construction that is happening in our mind. We create an abstract view of the world, and in this abstract view we come up with a version of reality that is simplified enough to explain, for instance, future events, but it is not too simple, since this would not allow us to explain anything specific or any smaller groups of events.
Causality is hence an abstraction that follows Occam's Razor. And since we all have our own version of Occam's Razor in our head, we often disagree when is comes to causality. This is merely related to the fact that everything dissolves under analysis. If we analyse any link between to events then the causal link can also be dissolved, or can become irrelevant. Ultimately, causality is a choice.
Take the example of medical studies where most studies build on a correlative design, testing how, for instance, taking Ibuprofen may help against the common cold. If I have a headache, and I take Ibuprofen, in most cases it may help me. But do I understand how it helps me? I may understand some parts of it, but I do not really understand it on a cellular level. There is again a certain level of abstraction.
What is now most relevant for causality is the mere fact that one thing can be explained by another thing. We do not need to understand all the nitty-gritty details of everything, and indeed this would be ultimately very hard on us. Instead, we need to understand whether taking one thing away prevents the other thing from happening. If I did not walk down the stairs, I would not have broken my leg.
Ever since Aristotle and his question ”What is its nature?”, we are nagged by the nitty-grittiness of true causality or deep causality. one could argue that there is a high road of causality, and a low road of causality. The high road allows us to explain everything on how two things or phenomena are linked. While some may reject this high road, many schools of thought consider it to be very relevant. Others prefer the low road of causality: May one thing or phenomena be causally linked to another thing or phenomena; if I take one away, will the other not happen? This automatically means that I have to make compromises of how much I understand about the world.
It is clear we do not need to understand everything. Our ancestors did not truly understand why walking out in the dark without a torch and a weapon - or better even in a larger group - might result in death in an area with many predators. Just knowing that staying in at night would keep them safe was good enough for them. It is also good enough for me.
Simple and complex Causality
Let us try to understand causal relations step by step. To this end, we may briefly differentiate two types of causal relations.
Statistical correlations imply causality if one variable (A) is actively driven by a variable (B). If B is taken away or changed, A changes as well or becomes non-existent. This relation is among the most abundantly known relation in statistics, but it has certain problems. First and foremost, two variables may be causally linked but the relation may be weak. Zinc may certainly help against the common cold, but it is not guaranteed that Zinc will cure us. It is a weak causal correlation.
Second, a causal relation of variable A and B may interact with a variable C, and further variables D, E, F etc. In this case, many people speak of complex relations. Complex relations can be causal, but they are still complex, and this complexity may confuse people. Lastly, statistical relations may be inflicted by biases, sample size restrictions, and many other challenges statistics face. These challenges are known, increasingly investigated, but often not solvable.
Structure the chaos: Normativity and plausibility

Building on the thought that our mind wanders to find causal relations, and then having the scientific experiment as a powerful tool, scientists started deriving and revising theories that were based on the experimental setups. Sometimes it was the other way around, as many theories were only later proven by observation or scientific experiments. Having causality explained by scientific theories created a combination that led to physical laws, societal paradigms and psychological models, among many other things.
Plausibility started its reign as a key criterion of modern science. Plausibility basically means that relations can only be causal if the relations are not only probable but also reasonable. Statistics takes care of the probability. But it is the human mind that derives reason out of data, making causality a deeply normative act. Counterfactual theories may later disprove our causality, which is why it was raised that we cannot know any truth, but we can approximate it. Our assumptions may still be falsified later.
So far, so good. It is worth noting that Aristoteles had some interesting metaphysical approaches to causality, as do Buddhists and Hindus. We will ignore these here for the sake of simplicity.
Hume's criteria for Causality
It seems obvious, but a necessary condition for causality is temporal order. Temporal causal chains can be defined as relations where an effect has a cause. An event A may directly follow an action B. In other words, A is caused by B. Quite often, we think that we see such causal relations rooted in a temporal chain. The complex debate on vaccinations and autism can be seen as such an example. The opponents of vaccinations think that the autism of their child was caused by a vaccination, while medical doctors argue that the onset of autism merely happened around the same time as the vaccination was given and thus is not causally linked. The temporal relation is in this case seen as a mere coincidence. Many such temporal relations are hence assumed, but our mind often deceives us, as we want to get fooled. We want order in the chaos, and for many people causality is bliss. History often tries to find causalities, yet as it was once claimed, history is written by the victorious, meaning it is subjective. Having a model that explains your reality is what many search for today and having some sort of a temporal causal chain seems to be one of the cravings of many human minds. Scientific experiments were invented to test such causalities, and human society evolved. Today it seems next to impossible to not know about gravity - in a sense we all know, yes - but the first physical experiments helped us proving the point. Hence did the scientific experiment help us to explore temporal causality, and medical trials can be seen as one of the highest propelled continuation of these.
We may however build on Hume, who wrote in his treatise of human nature the three criteria mentioned below. Paraphrasing his words, causality is contiguous in space and time, the cause is prior to the effect, and there is a constant union between cause and effect. It is worthwhile to consider the other criteria he mentioned.
1) Hume claims that the same cause always produces the same effect. In statistics, this pinpoints at the criterion of reproducibility, which is one of the backbones of the scientific experiment. This may be seen difficult in times of single case studies. While such studies are clearly relevant, their value is limited according to this criterion.
2) In addition, if several objects create the same effect, then there must be a uniting criterion among them causing the effect. A good example for this is weights on a balance. Several weights can be added up to have the same -counterbalancing- effect. One would need to pile a high number of feathers to get the same effect as, let’s say, 50 kg of weight (and it would be regrettable for the birds). Again, this is highly relevant for modern science, as looking for united criteria is a key goal in the amounts of data we often analyze these days.
3) If two objects have a different effect, there must be a reason that explains the difference. This third assumption of Hume is a direct consequence from the second one. What unites factors can be important, but equally important can be what differentiates factors. This is often the reason why we think there is a causal link between two things, when there clearly is not. Imagine some evil person gives you decaf coffee, while you are used to caffeine. The effect might be severe, and it is clear that the caffeine in the coffee that wakes you up differentiates this coffee from the decaffeinated one.
To summarize, causality is a mess in our brains. We are wrong about causality more often than we think, our brain is hardwired to find connections and often gets fooled into assuming causality. Equally, we often want to neglect causality, when it is clearly a fact. We are thus wrong quite often. In case of doubt, stick with Hume and the criteria mentioned above. Relying on these when analyzing correlations, ultimately, demands practice.
Additional Information
Hume, David. 1739. "A Treatise of Human Nature"
To train your ability to estimate correlation coefficients: https://www.guessthecorrelation.com/
The author of this entry is Henrik von Wehrden.