Difference between revisions of "Mixed Effect Models"
| (8 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [[File: | + | [[File:Quan dedu indu indi syst glob past pres futu.png|thumb|right|[[Design Criteria of Methods|Method Categorisation:]]<br> |
| − | + | '''Quantitative''' - Qualitative<br> | |
| − | <br | + | '''Deductive''' - '''Inductive'''<br> |
| − | + | '''Individual''' - '''System''' - '''Global'''<br> | |
| − | + | '''Past''' - '''Present''' - '''Future''']] | |
| − | + | '''In short:''' Mixed Effect Models are stastistical approaches that contain both fixed and random effects, i.e. models that analyse linear relations while decreasing the variance of other factors. | |
| − | + | <br> | |
| − | + | <br> | |
| − | + | <br><br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''In short:''' Mixed Effect Models contain both fixed and random effects, i.e. models that analyse linear relations while decreasing the variance of other factors. | ||
| − | |||
== Background == | == Background == | ||
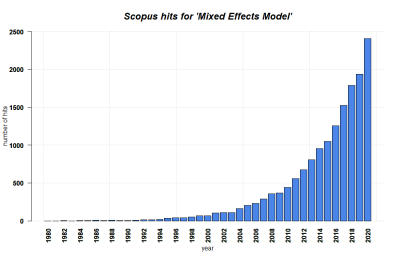
| + | [[File:Mixed Effects Model.png|400px|thumb|right|'''SCOPUS hits per year for Mixed Effects Models until 2020.''' Search terms: 'Mixed Effects Model' in Title, Abstract, Keywords. Source: own.]] | ||
Mixed Effect Models were a continuation of Fisher's introduction of random factors into the Analysis of Variance. Fisher saw the necessity not only to focus on what we want to know in a statistical design, but also what information we likely want to minimize in terms of their impact on the results. Fisher's experiments on agricultural fields focused on taming variance within experiments through the use of replicates, yet he was strongly aware that underlying factors such as different agricultural fields and their unique combinations of environmental factors would inadvertedly impact the results. He thus developed the random factor implementation, and Charles Roy Henderson took this to the next level by creating the necessary calculations to allow for linear unbiased estimates. These approaches allowed for the development of previously unmatched designs in terms of the complexity of hypotheses that could be tested, and also opened the door to the analysis of complex datasets that are beyond the sphere of purely deductively designed datasets. It is thus not surprising that Mixed Effect Models rose to prominence in such diverse disciplines as psychology, social science, physics, and ecology. | Mixed Effect Models were a continuation of Fisher's introduction of random factors into the Analysis of Variance. Fisher saw the necessity not only to focus on what we want to know in a statistical design, but also what information we likely want to minimize in terms of their impact on the results. Fisher's experiments on agricultural fields focused on taming variance within experiments through the use of replicates, yet he was strongly aware that underlying factors such as different agricultural fields and their unique combinations of environmental factors would inadvertedly impact the results. He thus developed the random factor implementation, and Charles Roy Henderson took this to the next level by creating the necessary calculations to allow for linear unbiased estimates. These approaches allowed for the development of previously unmatched designs in terms of the complexity of hypotheses that could be tested, and also opened the door to the analysis of complex datasets that are beyond the sphere of purely deductively designed datasets. It is thus not surprising that Mixed Effect Models rose to prominence in such diverse disciplines as psychology, social science, physics, and ecology. | ||
| + | |||
== What the method does == | == What the method does == | ||
| − | Mixed Effect Models are - mechanically speaking - one step further with regards to the combination of regression analysis and Analysis of Variance, as they can combine the strengths of both these approaches: '''Mixed Effects Models are able to incorporate both [[Data formats|categorical and/or continuous]] independent variables'''. Since Mixed Effect Models were further developed into [[Generalized Linear Models|Generalized Linear Mixed Effect Models]], they are also able to incorporate different distributions concerning the dependent variable. | + | Mixed Effect Models are - mechanically speaking - one step further with regards to the combination of [[Regression Analysis|regression analysis]] and Analysis of Variance, as they can combine the strengths of both these approaches: '''Mixed Effects Models are able to incorporate both [[Data formats|categorical and/or continuous]] independent variables'''. Since Mixed Effect Models were further developed into [[Generalized Linear Models|Generalized Linear Mixed Effect Models]], they are also able to incorporate different distributions concerning the dependent variable. |
Typically, the diverse algorithmic foundations to calculate Mixed Effect Models (such as maximum likelihood and restricted maximum likelihood) allow for more statistical power, which is why Mixed Effect Models often work slightly better compared to standard regressions. The main strength of Mixed Effect Models is however not how they can deal with fixed effects, but that they are able to incorporate random effects as well. '''The combination of these possibilities makes (generalised) Mixed Effect Models the swiss army knife of univariate statistics.''' No statistical model to date is able to analyse a broader range of data, and Mixed Effect Models are the gold standard in deductive designs. | Typically, the diverse algorithmic foundations to calculate Mixed Effect Models (such as maximum likelihood and restricted maximum likelihood) allow for more statistical power, which is why Mixed Effect Models often work slightly better compared to standard regressions. The main strength of Mixed Effect Models is however not how they can deal with fixed effects, but that they are able to incorporate random effects as well. '''The combination of these possibilities makes (generalised) Mixed Effect Models the swiss army knife of univariate statistics.''' No statistical model to date is able to analyse a broader range of data, and Mixed Effect Models are the gold standard in deductive designs. | ||
| − | Often, these models serve as a baseline for the whole scheme of analysis, and thus already help researchers to design and plan their whole data campaign. Naturally, then, these models are the heart of the analysis, and depending on the discipline, the interpretation can range from widely established norms (e.g. in medicine) to pushing the envelope in those parts of science where it is still unclear which variance is being tamed, and which cannot be tamed. Basically, all sorts of quantitative data can inform Mixed Effect Models, and software applications such as R, Python and SARS offer broad arrays of analysis solutions, which are still continuously developed. | + | Often, these models serve as a baseline for the whole scheme of analysis, and thus already help researchers to design and plan their whole data campaign. Naturally, then, these models are the heart of the analysis, and depending on the discipline, the interpretation can range from widely established norms (e.g. in medicine) to pushing the envelope in those parts of science where it is still unclear which variance is being tamed, and which cannot be tamed. Basically, all sorts of quantitative data can inform Mixed Effect Models, and software applications such as R, Python and SARS offer broad arrays of analysis solutions, which are still continuously developed. Mixed Effect Models are not easy to learn, and they are often hard to tame. Within such advanced statistical analysis, experience is key, and practice is essential in order to become versatile in the application of (generalised) Mixed Effect Models. |
| Line 40: | Line 32: | ||
== Normativity == | == Normativity == | ||
| − | Mixed Effect Models are the gold standard when it comes to reducing complexities into constructs, for better or worse. All variables that go into a Mixed Effect Model are normative choices, and these choices matter deeply. First of all, many people struggle to decide which variables are about fixed variance, and which variables are relevant as random variance. Second, how are these variables constructed - are they continuous or categorical, and if the latter, what is the reasoning behind the category levels? Designing Mixed Effect Modell studies is thus definitely a part of advanced statistics, and this is even harder when it comes to integrating non-designed datasets into a Mixed Effect Model framework. Care and experience are needed to evaluate sample sizes, variance across levels and variables. This brings us to the most crucial point: Model inspection. | + | Mixed Effect Models are the gold standard when it comes to reducing complexities into constructs, for better or worse. All variables that go into a Mixed Effect Model are normative choices, and these choices matter deeply. First of all, many people struggle to decide which variables are about fixed variance, and which variables are relevant as random variance. Second, how are these variables constructed - are they continuous or categorical, and if the latter, what is the reasoning behind the category levels? Designing Mixed Effect Modell studies is thus definitely a part of advanced statistics, and this is even harder when it comes to integrating non-designed datasets into a Mixed Effect Model [[Glossary|framework]]. Care and experience are needed to evaluate sample sizes, variance across levels and variables. This brings us to the most crucial point: Model inspection. |
'''Mixed Effect Models are built on a litany of preconditions, most of which most researchers choose to conveniently ignore.''' In my experience, this is more often than not ok, because it does not matter. Mixed Effect Models are - bless the maximum likelihood estimation - very sturdy. It is hard to find a model that does not have some predictive or explanatory value, even if hardly any pre-conditions are met. Still, this does not mean that we should ignore these. In order to sleep safe and sound at night, I am almost obsessed with model inspection, checking variance across levels, looking at the residuals, and looking for gaps and flaws in the model's fit. We should be really conservative to this end, because by focusing on fixed and random variance, we potentiate things that could go wrong. As I said, more often than not, this is not the case, but I propose to be super conservative when it comes to your model outcome. In order to get there, we need yet another thing: Model simplification. | '''Mixed Effect Models are built on a litany of preconditions, most of which most researchers choose to conveniently ignore.''' In my experience, this is more often than not ok, because it does not matter. Mixed Effect Models are - bless the maximum likelihood estimation - very sturdy. It is hard to find a model that does not have some predictive or explanatory value, even if hardly any pre-conditions are met. Still, this does not mean that we should ignore these. In order to sleep safe and sound at night, I am almost obsessed with model inspection, checking variance across levels, looking at the residuals, and looking for gaps and flaws in the model's fit. We should be really conservative to this end, because by focusing on fixed and random variance, we potentiate things that could go wrong. As I said, more often than not, this is not the case, but I propose to be super conservative when it comes to your model outcome. In order to get there, we need yet another thing: Model simplification. | ||
| − | Mixed Effect Models lead the forefront of statistics, and this might be the reason why the implementation of AIC (Akaike Information Criterion) as a parsimony-based evaluation criterion is more abundant here when compared to other statistical approaches. P-values fell widely out of fashion in many branches of science, as did the reporting of full models. Instead, model reduction based on information criteria approaches is on the rise, reporting parsimonious models that honour [[Why_statistics_matters#Occam.27s_razor | Occam's razor]]. Starting with the maximum model, these approaches reduce the model until it is the minimum adequate model - in other words, the model that is as simple as possible, but as complex as necessary. The AIC is about the equivalent of a p-value of 0.12, depending on the sample size, hence beware that the main question may be the difference from the null model. This links to the next point: Explanatory power. | + | Mixed Effect Models lead the forefront of statistics, and this might be the reason why the implementation of AIC (Akaike Information Criterion) as a parsimony-based evaluation criterion is more abundant here when compared to other statistical approaches. P-values fell widely out of fashion in many branches of science, as did the reporting of full models. Instead, model reduction based on information criteria approaches is on the rise, reporting parsimonious models that honour [[Why_statistics_matters#Occam.27s_razor | Occam's razor]]. Starting with the maximum model, these approaches reduce the model until it is the minimum adequate model - in other words, the model that is as simple as possible, but as complex as necessary. The AIC is about the equivalent of a p-value of 0.12, depending on the sample size, hence beware that the main question may be the difference from the null model. In other words, a model that is better from the Null model, but only just so based on the AIC, may not be significant because the p-value would be around 0.12. This links to the next point: Explanatory power. |
There has been some sort of a revival of r<sup>2</sup> values lately, mainly based on the suggestion of r<sup>2</sup> values that can be utilised for Mixed Effect Models. I deeply reject these approaches. First of all, Mixed Effect Models are not about how much the model explains, but whether the results are meaningfully different from the null model. I can understand that in a cancer study I would want to know how much my model may help people, hence an occasional glance of the fitted value against the original values may do no harm. However, r<sup>2</sup> in Mixed Effect Models is - to me - a step into the bad old days when we evaluated the worth of a model because of its ability to explain variance. This led to a lot of feeble discussions, of which I only mention here the debate on how good a model needs to be in terms of these values to be not bad, and vice versa. This is obviously a problem, and such normative judgements are a reason why statistics have such a bad reputation. Second, people are starting again to actually report their models based on the r<sup>2</sup> value, and even have their model selection not independent of the r<sup>2</sup> value. This is something that should be bygone, yet it is not. '''Beware of the r<sup>2</sup> value, it is only deceiving you in Mixed Effect Models.''' Third, r<sup>2</sup> values in Mixed Effect Models are deeply problematic because they cannot take the complexity of the random variance into account. Hence, r<sup>2</sup> values in Mixed Effect Models make us go back to the other good old days, when mean values were ruling the outcomes of science. Today, we are closer to an understanding where variance matters, and why would we embrace that. Ok, it comes with a longer learning curve, but I think that the good old reduction to the mean was nothing but mean. | There has been some sort of a revival of r<sup>2</sup> values lately, mainly based on the suggestion of r<sup>2</sup> values that can be utilised for Mixed Effect Models. I deeply reject these approaches. First of all, Mixed Effect Models are not about how much the model explains, but whether the results are meaningfully different from the null model. I can understand that in a cancer study I would want to know how much my model may help people, hence an occasional glance of the fitted value against the original values may do no harm. However, r<sup>2</sup> in Mixed Effect Models is - to me - a step into the bad old days when we evaluated the worth of a model because of its ability to explain variance. This led to a lot of feeble discussions, of which I only mention here the debate on how good a model needs to be in terms of these values to be not bad, and vice versa. This is obviously a problem, and such normative judgements are a reason why statistics have such a bad reputation. Second, people are starting again to actually report their models based on the r<sup>2</sup> value, and even have their model selection not independent of the r<sup>2</sup> value. This is something that should be bygone, yet it is not. '''Beware of the r<sup>2</sup> value, it is only deceiving you in Mixed Effect Models.''' Third, r<sup>2</sup> values in Mixed Effect Models are deeply problematic because they cannot take the complexity of the random variance into account. Hence, r<sup>2</sup> values in Mixed Effect Models make us go back to the other good old days, when mean values were ruling the outcomes of science. Today, we are closer to an understanding where variance matters, and why would we embrace that. Ok, it comes with a longer learning curve, but I think that the good old reduction to the mean was nothing but mean. | ||
| Line 51: | Line 43: | ||
== Outlook == | == Outlook == | ||
| − | In terms of Mixed Effect Models, language barriers and the norms of specific disciplines are rather strong. Explaining the basics of these advanced statistics to colleagues is an art in itself, just as the experience of researchers being versatile in [[Semi-structured Interview|Interview]]s cannot be reduced into a few hours of learning. Education in science needs to tackle this head on, and stop teaching statistics that are outdated and hardly published. I suggest that at least on a Master's level, in the long run, all students from the quantitative domain should be able to understand the preconditions and benefits of Mixed Effect Models, but this is something for the distant future. Today, PhD students being versatile in Mixed Effect Models are still outliers. Let us all hope that this statement will be outdated rather sooner than later. Mixed Effect Models are surely powerful and quite adaptable, and are increasingly becoming a part of normal science. Honouring the complexity of the world while still deriving value statements based on statistical analyses has never been more advanced on a broader scale. '''Still, statisticians need to | + | In terms of Mixed Effect Models, language barriers and the norms of specific disciplines are rather strong. Explaining the basics of these advanced statistics to colleagues is an art in itself, just as the experience of researchers being versatile in [[Semi-structured Interview|Interview]]s cannot be reduced into a few hours of learning. Education in science needs to tackle this head on, and stop teaching statistics that are outdated and hardly published. I suggest that at least on a Master's level, in the long run, all students from the quantitative domain should be able to understand the preconditions and benefits of Mixed Effect Models, but this is something for the distant future. Today, PhD students being versatile in Mixed Effect Models are still outliers. Let us all hope that this statement will be outdated rather sooner than later. Mixed Effect Models are surely powerful and quite adaptable, and are increasingly becoming a part of normal science. Honouring the complexity of the world while still deriving value statements based on statistical analyses has never been more advanced on a broader scale. '''Still, statisticians need to recognize the limitations of real world data, and researchers utilising these need to honour the preconditions and pitfalls of these analyses'''. Current science is in my perception far away from reporting reproducible analyses, meaning that one and the same dataset will be differently analysed by Mixed Effect Model approaches, partly based on experience, partly based on differences between disciplines, and probably also because of many other factors. Mixed Effect Models need to be consolidated and unified, which would make normale science probably better than ever. |
== Key Publications == | == Key Publications == | ||
Latest revision as of 11:37, 18 March 2024
Quantitative - Qualitative
Deductive - Inductive
Individual - System - Global
Past - Present - Future
In short: Mixed Effect Models are stastistical approaches that contain both fixed and random effects, i.e. models that analyse linear relations while decreasing the variance of other factors.
Contents
Background
Mixed Effect Models were a continuation of Fisher's introduction of random factors into the Analysis of Variance. Fisher saw the necessity not only to focus on what we want to know in a statistical design, but also what information we likely want to minimize in terms of their impact on the results. Fisher's experiments on agricultural fields focused on taming variance within experiments through the use of replicates, yet he was strongly aware that underlying factors such as different agricultural fields and their unique combinations of environmental factors would inadvertedly impact the results. He thus developed the random factor implementation, and Charles Roy Henderson took this to the next level by creating the necessary calculations to allow for linear unbiased estimates. These approaches allowed for the development of previously unmatched designs in terms of the complexity of hypotheses that could be tested, and also opened the door to the analysis of complex datasets that are beyond the sphere of purely deductively designed datasets. It is thus not surprising that Mixed Effect Models rose to prominence in such diverse disciplines as psychology, social science, physics, and ecology.
What the method does
Mixed Effect Models are - mechanically speaking - one step further with regards to the combination of regression analysis and Analysis of Variance, as they can combine the strengths of both these approaches: Mixed Effects Models are able to incorporate both categorical and/or continuous independent variables. Since Mixed Effect Models were further developed into Generalized Linear Mixed Effect Models, they are also able to incorporate different distributions concerning the dependent variable.
Typically, the diverse algorithmic foundations to calculate Mixed Effect Models (such as maximum likelihood and restricted maximum likelihood) allow for more statistical power, which is why Mixed Effect Models often work slightly better compared to standard regressions. The main strength of Mixed Effect Models is however not how they can deal with fixed effects, but that they are able to incorporate random effects as well. The combination of these possibilities makes (generalised) Mixed Effect Models the swiss army knife of univariate statistics. No statistical model to date is able to analyse a broader range of data, and Mixed Effect Models are the gold standard in deductive designs.
Often, these models serve as a baseline for the whole scheme of analysis, and thus already help researchers to design and plan their whole data campaign. Naturally, then, these models are the heart of the analysis, and depending on the discipline, the interpretation can range from widely established norms (e.g. in medicine) to pushing the envelope in those parts of science where it is still unclear which variance is being tamed, and which cannot be tamed. Basically, all sorts of quantitative data can inform Mixed Effect Models, and software applications such as R, Python and SARS offer broad arrays of analysis solutions, which are still continuously developed. Mixed Effect Models are not easy to learn, and they are often hard to tame. Within such advanced statistical analysis, experience is key, and practice is essential in order to become versatile in the application of (generalised) Mixed Effect Models.
Strengths & Challenges
The biggest strength of Mixed Effect Models is how versatile they are. There is hardly any part of univariate statistics that can not be done by Mixed Effect Models, or to rephrase it, there is hardly any part of advanced statistics that - even if it can be made by other models - cannot be done better by Mixed Effect Models. They surpass the Analyis of Variance in terms of statistical power, eclipse Regressions by being better able to consider the complexities of real world datasets, and allow for a planning and understanding of random variance that brings science one step closer to acknowledge that there are things that we want to know, and things we do not want to know.
Take the example of many studies in medicine that investigate how a certain drug works on people to cure a disease. To this end, you want to know the effect the drug has on the prognosis of the patients. What you do not want to know is whether people are worse off if they are older, have a lack of exercise or an unhealthy diet. All these single effects do not matter for you, because it is well known that the prognosis often gets worse with higher age, and factors such as lack of exercise and unhealthy diet choices. What you may want to know, is whether the drug works better or worse in people that have unhealthy diet choice, are older or lack regular exercise. These interaction can be meaningfully investigated by Mixed Effect Models. All positive factors' variance is minimised, while the effect of the drug as well as its interactions with the other factors can be tested. This makes Mixed Effect Models so powerful, as you can implement them in a way that allows to investigate quite complex hypotheses or questions.
The greatest disadvantage of Mixed Effect Models is the level of experience that is necessary to implement them in a meaningful way. Designing studies takes a lot of experience, and the current form of peer-review does often not allow to present the complex thinking that goes into the design of advanced studies (Paper BEF China design). There is hence a discrepancy in how people implement studies, and how other researchers can understand and emulate these approaches. Mixed Effect Models are also an example where textbook knowledge is not saturated yet, hence books are rather quickly outdated, and also often do not offer exhausting examples to real life problems researchers may face when designing studies. Medicine and psychology are offering growing resources to this end, since here the preregistration of studies due to the reproducibility crisis offers a glimpse in the design of scientific studies.
The lack of experience in how to design and conduct Mixed Effect Models-driven studies leads to the critical reality that more often than not, there are flaws in the application of the method. While this got gradually less bad over time, it is still a matter of debate whether every published study with these models does justice to the original idea. Especially around the millennium, there was almost a hype in some branches of science regarding how fancy Mixed Effect Models were considered, and not all applications were sound and necessary. Mixed Effect Models can also make the world more complicated than it is: sometimes a regression is just a regression is just a regression.
Normativity
Mixed Effect Models are the gold standard when it comes to reducing complexities into constructs, for better or worse. All variables that go into a Mixed Effect Model are normative choices, and these choices matter deeply. First of all, many people struggle to decide which variables are about fixed variance, and which variables are relevant as random variance. Second, how are these variables constructed - are they continuous or categorical, and if the latter, what is the reasoning behind the category levels? Designing Mixed Effect Modell studies is thus definitely a part of advanced statistics, and this is even harder when it comes to integrating non-designed datasets into a Mixed Effect Model framework. Care and experience are needed to evaluate sample sizes, variance across levels and variables. This brings us to the most crucial point: Model inspection.
Mixed Effect Models are built on a litany of preconditions, most of which most researchers choose to conveniently ignore. In my experience, this is more often than not ok, because it does not matter. Mixed Effect Models are - bless the maximum likelihood estimation - very sturdy. It is hard to find a model that does not have some predictive or explanatory value, even if hardly any pre-conditions are met. Still, this does not mean that we should ignore these. In order to sleep safe and sound at night, I am almost obsessed with model inspection, checking variance across levels, looking at the residuals, and looking for gaps and flaws in the model's fit. We should be really conservative to this end, because by focusing on fixed and random variance, we potentiate things that could go wrong. As I said, more often than not, this is not the case, but I propose to be super conservative when it comes to your model outcome. In order to get there, we need yet another thing: Model simplification.
Mixed Effect Models lead the forefront of statistics, and this might be the reason why the implementation of AIC (Akaike Information Criterion) as a parsimony-based evaluation criterion is more abundant here when compared to other statistical approaches. P-values fell widely out of fashion in many branches of science, as did the reporting of full models. Instead, model reduction based on information criteria approaches is on the rise, reporting parsimonious models that honour Occam's razor. Starting with the maximum model, these approaches reduce the model until it is the minimum adequate model - in other words, the model that is as simple as possible, but as complex as necessary. The AIC is about the equivalent of a p-value of 0.12, depending on the sample size, hence beware that the main question may be the difference from the null model. In other words, a model that is better from the Null model, but only just so based on the AIC, may not be significant because the p-value would be around 0.12. This links to the next point: Explanatory power.
There has been some sort of a revival of r2 values lately, mainly based on the suggestion of r2 values that can be utilised for Mixed Effect Models. I deeply reject these approaches. First of all, Mixed Effect Models are not about how much the model explains, but whether the results are meaningfully different from the null model. I can understand that in a cancer study I would want to know how much my model may help people, hence an occasional glance of the fitted value against the original values may do no harm. However, r2 in Mixed Effect Models is - to me - a step into the bad old days when we evaluated the worth of a model because of its ability to explain variance. This led to a lot of feeble discussions, of which I only mention here the debate on how good a model needs to be in terms of these values to be not bad, and vice versa. This is obviously a problem, and such normative judgements are a reason why statistics have such a bad reputation. Second, people are starting again to actually report their models based on the r2 value, and even have their model selection not independent of the r2 value. This is something that should be bygone, yet it is not. Beware of the r2 value, it is only deceiving you in Mixed Effect Models. Third, r2 values in Mixed Effect Models are deeply problematic because they cannot take the complexity of the random variance into account. Hence, r2 values in Mixed Effect Models make us go back to the other good old days, when mean values were ruling the outcomes of science. Today, we are closer to an understanding where variance matters, and why would we embrace that. Ok, it comes with a longer learning curve, but I think that the good old reduction to the mean was nothing but mean.
Another very important point regarding Mixed Effect Models is that they - probably more than any statistical method - remark the point where experts in one method (say for example interviews) now needed to learn how to conduct interviews as a scientific method, but also needed to learn advanced statistics in the form of Mixed Effect Models. This creates a double burden, and while learning several methods can be good to embrace a more diverse understanding, it is also challenging, and highlights a new development. Today, statistical analysis are increasingly outsourced to experts, and I consider this to be a generally good development. In my own experience, it takes a few thousand hours to become versatile at Mixed Effect Models, and modern science is increasingly built on collaboration.
Outlook
In terms of Mixed Effect Models, language barriers and the norms of specific disciplines are rather strong. Explaining the basics of these advanced statistics to colleagues is an art in itself, just as the experience of researchers being versatile in Interviews cannot be reduced into a few hours of learning. Education in science needs to tackle this head on, and stop teaching statistics that are outdated and hardly published. I suggest that at least on a Master's level, in the long run, all students from the quantitative domain should be able to understand the preconditions and benefits of Mixed Effect Models, but this is something for the distant future. Today, PhD students being versatile in Mixed Effect Models are still outliers. Let us all hope that this statement will be outdated rather sooner than later. Mixed Effect Models are surely powerful and quite adaptable, and are increasingly becoming a part of normal science. Honouring the complexity of the world while still deriving value statements based on statistical analyses has never been more advanced on a broader scale. Still, statisticians need to recognize the limitations of real world data, and researchers utilising these need to honour the preconditions and pitfalls of these analyses. Current science is in my perception far away from reporting reproducible analyses, meaning that one and the same dataset will be differently analysed by Mixed Effect Model approaches, partly based on experience, partly based on differences between disciplines, and probably also because of many other factors. Mixed Effect Models need to be consolidated and unified, which would make normale science probably better than ever.
Key Publications
The author of this entry is Henrik von Wehrden.