Difference between revisions of "Experiments"
| Line 52: | Line 52: | ||
The ANOVA builds on a constructed world, where factor levels are like all variables constructs, which might be prone to errors or misconceptions. We should therefore realize that a non-significant result might also be related to the factor level construction. Yet a potential flaw can also range beyond implausible results, since ANOVAs do not necessarily create valid knowledge. If the underlying theory is imperfect, then we might confirm a hypothesis that is overall wrong. Hence the strong benefit of the ANOVA - the systematic testing of hypothesis - may equally be also its weakest point, as science develops, and previous hypothesis might have been imperfect if not wrong. | The ANOVA builds on a constructed world, where factor levels are like all variables constructs, which might be prone to errors or misconceptions. We should therefore realize that a non-significant result might also be related to the factor level construction. Yet a potential flaw can also range beyond implausible results, since ANOVAs do not necessarily create valid knowledge. If the underlying theory is imperfect, then we might confirm a hypothesis that is overall wrong. Hence the strong benefit of the ANOVA - the systematic testing of hypothesis - may equally be also its weakest point, as science develops, and previous hypothesis might have been imperfect if not wrong. | ||
| − | Furthermore, many researchers use the ANOVA today in an inductive sense. With more and more data becoming available, even from completely undersigned sampling sources, the ANOVA becomes the analysis of choice if the difference between different factor levels is investigated for a continuous variable. Due to the emergence of big data, these applications could be seen critical, since no real hypothesis are being tested. Instead, the statistician becomes a gold digger, searching the vastness of the available data for patterns, [[Causality#Correlation_is_not_Causality|may these be causal or not]]. While there are numerous benefits, this is also a source of problems. Non-designed datasets will for instance not be able to test for the impact a drug might have on a certain diseases. This is a problem, as systematic knowledge production is almost assumed within the ANOVA, but its application these days is far away from it. The inductive and the deductive world become intertwined, and this poses a risk for the validity of scientific results. | + | Furthermore, many researchers use the ANOVA today in an inductive sense. With more and more data becoming available, even from completely undersigned sampling sources, the ANOVA becomes the analysis of choice if the difference between different factor levels is investigated for a continuous variable. Due to the [[Glossary|emergence]] of big data, these applications could be seen critical, since no real hypothesis are being tested. Instead, the statistician becomes a gold digger, searching the vastness of the available data for patterns, [[Causality#Correlation_is_not_Causality|may these be causal or not]]. While there are numerous benefits, this is also a source of problems. Non-designed datasets will for instance not be able to test for the impact a drug might have on a certain diseases. This is a problem, as systematic knowledge production is almost assumed within the ANOVA, but its application these days is far away from it. The inductive and the deductive world become intertwined, and this poses a risk for the validity of scientific results. |
For more on the Analysis of Variance, please refer to the [[ANOVA]] entry. | For more on the Analysis of Variance, please refer to the [[ANOVA]] entry. | ||
Revision as of 23:17, 13 June 2021
Note: This entry revolves mostly around laboratory experiments. For more details on experiments, please refer to the entries on Experiments and Hypothesis Testing, Case studies and Natural experiments as well as Field experiments.
Contents
History of laboratory experiments
Experiments describe the systematic and reproducible design to test specific hypothesis.
Starting with Francis Bacon there was the theoretical foundation to shift previously widely un-systematic experiments into a more structured form. With the rise of disciplines in the enlightenment experiments thrived, also thanks to an increasing amount of resources available in Europe due to the Victorian age and other effects of colonialism. Deviating from more observational studies in physics, astronomy, biology and other fields, experiments opened the door to the wide testing of hypothesis. All the while Mill and others build on Bacon to derive the necessary basic debates about so called facts, building the theoretical basis to evaluate the merit of experiments. Hence these systematic experimental approaches aided many fields such as botany, chemistry, zoology, physics and much more, but what was even more important, these fields created a body of knowledge that kickstarted many fields of research, and even solidified others. The value of systematic experiments, and consequently systematic knowledge created a direct link to practical application of that knowledge. The scientific method -called with the ignorant recognition of no other methods beside systematic experimental hypothesis testing as well as standardisation in engineering- hence became the motor of both the late enlightenment as well as the industrialisation, proving a crucial link between basically enlightenment and modernity.
Due to the demand of systematic knowledge some disciplines ripened, meaning that own departments were established, including the necessary laboratory spaces to conduct experiments. The main focus to this end was to conduct experiments that were as reproducible as possible, meaning ideally with a 100 % confidence. Laboratory conditions thus aimed at creating constant conditions and manipulating ideally only one or few parameters, which were then manipulated and therefore tested systematically. Necessary repetitions were conducted as well, but of less importance at that point. Much of the early experiments were hence experiments that were rather simple but produced knowledge that was more generalisable. There was also a general tendency of experiments either working or not, which is up until today a source of great confusion, as an trial and error approach -despite being a valid approach- is often confused with a general mode of “experimentation”. In this sense, many people consider preparing a bike without any knowledge about bikes whatsoever as a mode of “experimentation”. We therefore highlight that experiments are systematic. The next big step was the provision of certainty and ways to calculate uncertainty, which came with the rise of probability statistics.
First in astronomy, but then also in agriculture and other fields the notion became apparent that our reproducible settings may sometimes be hard to achieve. Error of measurements in astronomy was a prevalent problem of optics and other apparatus in the 18th and 19th century, and Fisher equally recognised the mess -or variance- that nature forces onto a systematic experimenter. The laboratory experiment was hence an important step towards a systematic investigation of specific hypothesis, underpinned by newly established statistical approaches.
Key concepts of laboratory experiments – sampling data in experimental designs
Statistics enabled replication as a central principle that was first implemented into laboratory experiments. Replicates are basically the repetition of the same experiment in order to derive whether an effect is constant or has a specific variance. This variance is an essential feature of many natural phenomena, such as plant growth, but also caused by systematic errors such as measurement uncertainty. Hence the validity and reliability of an experiment could be better tamed.
Within laboratory experiment, control of certain variables is essential, as this is the precondition to statistically test the few variables that are in the focus of the investigation. Control of variables means to this end, that such controlled variables are being held constant, thus the variables that are being tested are leading to the variance in the analysis. Consequently, such experiments are also known controlled experiments.
By increasing the sample size, it is possible to test the hypothesis according to a certain probability, and to generate a measure of reliability. The larger the sample is, the higher is the statistical power to be regarded. Within controlled experiments the so-called treatments are typically groups, where continuous gradients are converted into factors. An example would be the amount of fertilizer, which can be constructed into “low”, “middle” and ”high” amount of fertilizer. This allows a systematic testing based on a smaller number of replicates. The number of treatments or factor levels defines the degrees of freedom of an experiment. The more levels are tested, the higher does the number of samples need to be, which can be calculated based on the experimental design. Therefore, scientists design their experiments very clearly before conducting the study, and within many scientific fields are such experimental designs even submitted to a precheck and registration to highlight transparency and minimize potential flaws or manipulations.
Such experimental designs can even become more complicated when interaction effects are considered. In such experiments, two different factors are manipulated and the interactions between the different levels are investigated. A standard example would be quantification of plant growth of a specific plant species under different watering levels and amounts of fertilizer. Taken together, it is vital for researchers conducting experiments to be versatile in the diverse dimensions of the design of experiments. Sample size, replicates, factor levels, degrees of freedom and statistical power are all to be considered when conducting an experiment. Becoming versatile in designing such studies takes practice.
How do I compare more than two groups ?
People knew about the weather, soils, fertilizer and many other things, and this is how they could maximize their agricultural yield. Or did they? People had local experience but general patterns of what contributes to a high yield of a certain crop were comparably anecdotal. Before Fisher arrived in agriculture, statistics was less applied. There were applied approaches, which is why the t-test is called student test. However, most statisticians back then did statistics, and the agricultural folks did agriculture.
Fisher put these two things together, and they became one. His core question was how to increase yield. For this, there was quite an opportunity at that time. Industrialisation contributed to an exponential growth of many, many things (among them artificial fertilizer) which enabled people to grow more crops and increase yield. Fisher was the one who made the question of how to increase yield systematically. By developing the Analysis of Variance (ANOVA), he enabled comparison of more than two groups in terms of a continuous phenomenon. He did this in a way that you could, for example, compare which fertilizer would produce the highest yield. With Fisher's method, one could create an experimental design, fertilize some plants a little bit, some plants more, and others not at all. This enabled research to compare what is called different treatments, which are the different levels of fertilizer; in this case: none, a little, and more fertilizer. This became a massive breakthrough in agriculture, and Fisher's basic textbook became one of the most revolutionary methodological textbooks of all time, changing agriculture and enabling exponential growth of the human population.
Other disciplines had a similar problem when it came to comparing groups, most prominently medicine and psychology. Both disciplines readily accepted the ANOVA as their main method in early systematic experiments, since comparing different treatments is quite relevant when it comes to their experimental setups. Antibiotics were one of the largest breakthroughs in modern medicine, but how should one know which antibiotics work best to cure a specific disease? The ANOVA enables a clinical trial, and with it a systematic investigation into which medicine works bests against which disease. This was quite important, since an explanation on how this actually works was often missing up until today. Much of medical research does not offer a causal understanding, but due to the statistical data, at least patterns can be found that enable knowledge. This knowledge is, however, mostly not causal, which is important to remember. The ANOVA was an astounding breakthrough, since it enabled pattern recognition without demanding a causal explanation.
Analysis of Variance
The ANOVA is one key analysis tool of laboratory experiments - but also other experiments as we shall see later. This statistical test is - mechanically speaking - comparing the means of more than two groups by extending the restriction of the t-test. Comparing different groups became thus a highly important procedure in the design of experiments, which is, apart from laboratories, also highly relevant in greenhouse experiments in ecology, where conditions are kept stable through a controlled environment.
The general principle of the ANOVA is rooted in hypothesis testing. An idealized null hypothesis is formulated against which the data is being tested. If the ANOVA gives a significant result, then the null hypothesis is rejected, hence it is statistically unlikely that the data confirms the null hypothesis. As one gets an overall p-value, it can be thus confirmed whether the different groups differ overall. Furthermore, the ANOVA allows for a measure beyond the p-value through the sum of squares calculations which derive how much is explained by the data, and how large in relation the residual or unexplained information is.
Preconditions
Regarding the preconditions of the ANOVA, it is important to realize that the data should ideally be normally distributed on all levels, which however is often violated due to small sample sizes. Since a non-normal distribution may influence the outcome of the test, boxplots are a helpful visual aid, as these allow for a simple detection tool of non-normal distribution levels.
Equally should ideally the variance be comparable across all levels, which is called homoscedastic. What is also important is the criteria of independence, meaning that samples of factor levels should not influence each other. For this reason are for instance in ecological experiments plants typically planted in individual pots. In addition does the classical ANOVA assume a balanced design, which means that all factor levels have an equal sample size. If some factor levels have less samples than others, this might pose interactions in terms of normals distribution and variance, but there is another effect at play. Larger sample sizes on one factor level may create a disbalance, where factor levels with larger samples pose a larger influence on the overall model result.
One way and two way ANOVA
Single factor analysis that are also called 'one-way ANOVAs' investigate one factor variable, and all other variables are kept constant. Depending on the number of factor levels these demand a so called randomisation, which is necessary to compensate for instance for microclimatic differences under lab conditions.
Designs with multiple factors or 'two way ANOVAs' test for two or more factors, which then demands to test for interactions as well. This increases the necessary sample size on a multiplicatory scale, and the degrees of freedoms may dramatically increase depending on the number of factors levels and their interactions. An example of such an interaction effect might be an experiment where the effects of different watering levels and different amounts of fertiliser on plant growth are measured. While both increased water levels and higher amounts of fertiliser right increase plant growths slightly, the increase of of both factors jointly might lead to a dramatic increase of plant growth.
Interpretation of ANOVA
Boxplots provide a first visual clue to whether certain factor levels might be significantly different within an ANOVA analysis. If one box within a boxplot is higher or lower than the median of another factor level, then this is a good rule of thumb whether there is a significant difference. When making such a graphically informed assumption, we have to be however really careful if the data is normally distributed, as skewed distributions might tinker with this rule of thumb. The overarching guideline for the ANOVA are thus the p-values, which give significance regarding the difference between the different factor levels.
It can however also be relevant to compare the difference between specific groups, which is made by a posthoc test. A prominent example is the Tukey Test, where two factor levels are compared, and this is done iteratively for all factor level combinations. Since this poses a problem of multiple testing, there is a demand for a Bonferonni correction to adjust the p-value. Mechanically speaking, this is comparable to conducting several t-tests between two factor level combinations, and adjusting the p-values to consider the effects of multiple testing.
Challenges of ANOVA experiments
The ANOVA builds on a constructed world, where factor levels are like all variables constructs, which might be prone to errors or misconceptions. We should therefore realize that a non-significant result might also be related to the factor level construction. Yet a potential flaw can also range beyond implausible results, since ANOVAs do not necessarily create valid knowledge. If the underlying theory is imperfect, then we might confirm a hypothesis that is overall wrong. Hence the strong benefit of the ANOVA - the systematic testing of hypothesis - may equally be also its weakest point, as science develops, and previous hypothesis might have been imperfect if not wrong.
Furthermore, many researchers use the ANOVA today in an inductive sense. With more and more data becoming available, even from completely undersigned sampling sources, the ANOVA becomes the analysis of choice if the difference between different factor levels is investigated for a continuous variable. Due to the emergence of big data, these applications could be seen critical, since no real hypothesis are being tested. Instead, the statistician becomes a gold digger, searching the vastness of the available data for patterns, may these be causal or not. While there are numerous benefits, this is also a source of problems. Non-designed datasets will for instance not be able to test for the impact a drug might have on a certain diseases. This is a problem, as systematic knowledge production is almost assumed within the ANOVA, but its application these days is far away from it. The inductive and the deductive world become intertwined, and this poses a risk for the validity of scientific results.
For more on the Analysis of Variance, please refer to the ANOVA entry.
Examples
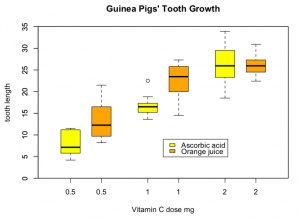
Toothgrowth of guinea pigs
#To find out, what the ToothGrowth data set is about: ?ToothGrowth
#The code is partly from boxplot help (?boxplot). If you like to know the meaning of the code below, you can look it up there
data(ToothGrowth)
# to create a boxplot
boxplot(len ~ dose, data = ToothGrowth,
boxwex = 0.25,
at = 1:3 - 0.2,
subset = supp == "VC", col = "yellow",
main = "Guinea Pigs’ Tooth Growth",
xlab = "Vitamin C dose mg",
ylab = "tooth length",
xlim = c(0.5, 3.5), ylim = c(0, 35), yaxs = "i")
boxplot(len ~ dose, data = ToothGrowth, add = TRUE,
boxwex = 0.25,
at = 1:3 + 0.2,
subset = supp == "OJ", col = "orange")
legend(2, 9, c("Ascorbic acid", "Orange juice"),
fill = c ("yellow", "orange"))
#to apply an ANOVA
model1<-aov(len ~ dose*supp, data = ToothGrowth)
summary(model1)
#Interaction is significant
Insect sprays
#To find out, what the InsectSprays data set is about: ?InsectSprays
data(InsectSprays)
attach(InsectSprays)
tapply(count, spray, length)
boxplot(count~spray)
# can you guess which sprays are effective by looking at the boxplot?
# to find out which sprays differ significantly without applying many t-tests, you can use a postdoc test
model2<-aov(count~spray)
TukeyHSD(model2)
# compare the results to the boxplot if you like
Balanced vs. unbalanced designs
There is such a thing as a perfect statistical design, and then there is reality.
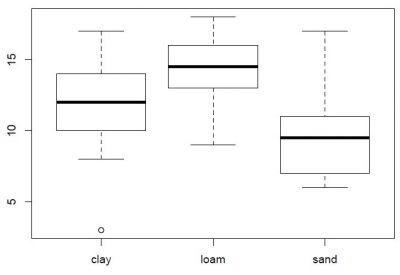
Statistician often think in so called balanced designs, which indicate that the samples across several levels were sampled with the same intensity. Take three soil types, which were sampled for their agricultural yield in a mono crop. Ideally, all soil types should be investigated with the same amount of samples. If we would have three soil types -clay, loam, and sand- we should not sample sand 100 times, and clay only 10 times. If we did, our knowledge about sandy soils would be much higher compared to clay soil. This does not only represent a problem when it comes to the general knowledge, but also creates statistical problems.
First of all, the sandy soil would be represented much more in an analysis that does not or cannot take such an unbalanced sampling into account.
Second, many analysis have assumptions about a certain statistical distribution, most notably the normal distribution, and a smaller sample may not show a normal distribution, which in turn may create a bias within the analysis. In order to keep this type of bias at least constant across all levels, we either need a balanced design, or use an analysis that compensates for such unbalanced designs. This analysis was realised with so called Type III ANOVA, which can take different sampling intensities into account. Type III ANOVA corrects for the error that is potentially inferred due to differing sample density, that means number of samples per level.
Why is this relevant, you ask?
Because the world is messy. Plants die. So do animals. Even people die. It is sad. For a statistician particularly because it makes one miss out on samples, and dis-balances your whole design. And while this may not seem like a bad problem for laypeople, for statistician it is a real mess. Therefore the ways to deal with unbalanced designs were such a breakthrough, because they finally allowed the so neatly thinking statisticians to not only deal with the nitty-gritty mess of unbalanced designs, but with real world data.
While experimental designs can be generated to be balanced, the real world data is almost never balanced. Hence, the ANOVA dealing with unbalanced data was one substantial step towards analysing already existing data, which is extraordinary, since the ANOVA was originally designed as the sharpest tool of the quantitative branch of science. Suddenly we were enabled to analyse real world data, often rather large, and often without a clear predefined hypothesis.
I (Henrik) propose that this was a substantial contributon away from a clear distinction between inductive or deductive research. People started analysing data, but following the tradition of their discipline still had to come up with hypotheses, even if they only saw patterns after the analysis. While this paved the road to machine learning, scientific theory still has to recover from it, I say. Rule of thumb: Always remember that you have hypotheses before a study, everything else is inductive, which is also ok.
External Links
Articles
The Enlightenment: Also some kind of repetition
History of experiments in astronomy: A short but informative text
History of the Clinical Laboratory: A brief article
Laboratory Experiments: Some strengths and weaknesses
Trial and Error Approach: A very detailed explanation
Replicates: A detailed explanation
Sample size: Why it matters!
Treatments in Experiments: Some definitions for terms in experimental design
Interaction effects: An article with many examples
Ronald Fisher: A short biography
ANOVA in pharmaceutical and healthcare: Examples from real life
ANOVA: An introduction
One-Way ANOVA vs. Two-Way ANOVA: Some different types
Homoscedasticity: A quick explanation
Posthoc Tests: A list of different types
The Tukey Test: A short article about this posthoc test
Videos
The Scientific Method: An insight into Bacons, Galileos and Descartes thoughts
Controlled Experiments: A short example from biology
What is good experiment?: A very short and simple video
Degrees of Freedom: A detailed explanation
Ronald Fisher: A short introduction
ANOVA: A detailed explanation
One-Way ANOVA vs. Two-Way ANOVA: A short comparison
The author of this entry is Henrik von Wehrden.