A/B Testing
THIS ARTICLE IS STILL IN EDITING MODE
Contents
A/B Testing in a nutshell
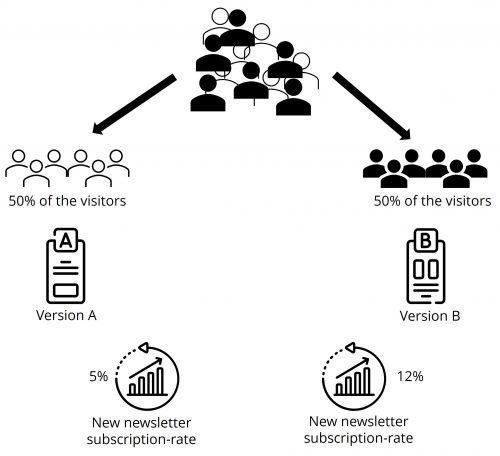
A/B testing, also known as split testing or bucket testing, is a method used to compare the performance of two versions of a product or content. This is done by randomly assigning similarly sized audiences to view either the control version (version A) or the treatment version (version B) over a set period of time and measuring their effect on a specific metric, such as clicks, conversions, or engagement. This method is commonly used in the optimization of websites, where the control version is the default version, while the treatment version is changed in a single variable, such as the content of text, colors, shapes, size or positioning of elements on the website.
An important advantage of A/B testing is its ability to establish causal relationships with a high degree of probability, which can transform decision making from an intuitive process to a scientific, evidence-based process. To ensure the trustworthiness of the results of A/B tests, the scheme of scientific experiments is followed, consisting of a planning phase, an execution phase, and an evaluation phase.
Planning Phase
During the planning phase, a goal and hypothesis are formulated, and a study design is developed that specifies the sample size, the duration of the study, and the metrics to be measured. This phase is crucial for ensuring the reliability and validity of the test.
Goal Definition
The goal identifies problems or optimization potential to improve the software product. For example, in the case of a website, the goal could be to increase newsletter subscriptions or improve the conversion rate through changing parts of the website.
Hypotheses Formulation
To determine if a particular change is better than the default version, a two-sample hypothesis test is conducted to determine if there are statistically significant differences between the two samples (version A and B). This involves stating the null hypothesis and the alternative hypothesis.
From the perspective of an A/B test, the null hypothesis states that there is no difference between the control and treatment group, while the alternative hypothesis states that there is a difference between the two groups which is influenced by a non-random cause.
In most cases, it is not known a priori whether the discrepancy in the results between A and B is in favor of A or B. Therefore, the alternative hypothesis should consider the possibility that both versions A and B have different levels of efficiency. In order to account for this, a two-sided test is typically preferred for the subsequent evaluation.
For example:
"To fix the problem that there are hardly any subscriptions for my newsletter, I will put the sign-up box higher up on the website."
Goal: Increase the newsletter subscriptions on the website.
H0: There are no significant changes in the number of new newsletter subscribers between the control and treatment versions.
H1: There are significant changes in the number of new newsletter subscribers between the control and treatment versions.
Minimizing Confounding Variables
In order to obtain accurate results, it is important to minimize confounding variables before the A/B test is conducted. This involves determining an appropriate sample size, tracking the right users, collecting the right metrics, and ensuring that the randomization unit is adequate.
The sample size is determined by the percentage of users included in the test variants (control and treatment) and the duration of the experiment. As the experiment runs for a longer period of time, more visitors are exposed to the variants, resulting in an increase in the sample size. Because many external factors vary over time, it is important to randomize over time by running the control and treatment variants simultaneously at a fixed percentage throughout the experiment. Thereby the goal is to obtain adequate statistical power, where the statistical power of an experiment is the probability of detecting a particular effect if it exists. In practice, one can assign any percentages to the control and treatment, but 50% gives the experiment maximum statistical power.
Furthermore, it is important to analyze only the subset of the population/users that were potentially affected. For example, in an A/B test aimed at optimizing newsletter subscriptions, it would be appropriate to exclude individuals who were already subscribed to the newsletter, as they would not have been affected by the changes made to the subscription form.
Additionally, the metrics used in the experiment should be carefully chosen based on their relevance to the hypotheses being tested. For example, in the case of an e-commerce site, metrics such as newsletter subscriptions and revenue per user may be of interest, as they are directly related to the goal of the test. However, it is important to avoid considering too many metrics at once, as this can increase the risk of miscorrelation.
Execution Phase
The execution phase involves implementing the study design, collecting data, and monitoring the study to ensure it is conducted according to the plan. During this phase, users are randomly assigned to the control or treatment group ensuring that the study is conducted in a controlled and unbiased manner.
Evaluation Phase
The evaluation phase involves analyzing the data collected during the study and interpreting the results. This phase is crucial for determining the statistical significance of the results and drawing valid conclusions about whether there was a statistical significant difference between the treatment group and the control group. One commonly used method is calculating the p-value of the statistical test, or by using Bayes' theorem calculating the probability that the treatment had a positive effect based on the observed data and the prior beliefs about the treatment.
Depending on the type of data being collected different statistical tests should be considered. For example, when dealing with discrete metrics such as click-through rate, the Fisher exact test can be used to calculate the exact p-value, while the chi-squared test may be more appropriate for larger sample sizes.
In the case of continuous metrics, such as average revenue per user, the t-test or Welch's t-test may be used to determine the significance of the treatment effect. However, these tests assume that the data is normally distributed, which may not always be the case. In cases where the data is not normally distributed, nonparametric tests such as the Wilcoxon rank sum test may be more appropriate.
Advantages and Limitations of A/B Testing
Advantages A/B testing has several advantages over traditional methods of evaluating the effectiveness of a product or design. First, it allows for a more controlled and systematic comparison of the treatment and control version. Second, it allows for the random assignment of users to the treatment and control groups, reducing the potential for bias. Third, it allows for the collection of data over a period of time, which can provide valuable insights into the long-term effects of the treatment.
Limitations Despite its advantages, A/B testing also has some limitations. For example, it is only applicable to products or designs that can be easily compared in a controlled manner. In addition, the results of an A/B test may not always be generalizable to the broader population, as the sample used in the test may not be representative of the population as a whole. Furthermore, it is not always applicable, as it requires a clear separation between control and treatment, and it may not be suitable for testing complex products or processes, where the relationship between the control and treatment versions is not easily defined or cannot be isolated from other factors that may affect the outcome.
Overall, A/B testing is a valuable tool for evaluating the effects of software or design changes. By setting up a controlled experiment and collecting data, we can make evidence-based decisions about whether a change should be implemented.
Key Publications
Kohavi, Ron, and Roger Longbotham. “Online Controlled Experiments and A/B Testing.” Encyclopedia of Machine Learning and Data Mining, 2017, 922–29. https://doi.org/10.1007/978-1-4899-7687-1_891Add to Citavi project by DOI.
Koning, Rembrand, Sharique Hasan, and Aaron Chatterji. “Experimentation and Start-up Performance: Evidence from A/B Testing.” Management Science 68, no. 9 (September 2022): 6434–53. https://doi.org/10.1287/mnsc.2021.4209Add to Citavi project by DOI.
Siroker, Dan, and Pete Koomen. A / B Testing: The Most Powerful Way to Turn Clicks Into Customers. 1st ed. Wiley, 2015.
The author of this entry is Malte Bartels. Edited by Milan Maushart