Factor Analysis
THIS ARTICLE IS STILL IN EDITING MODE
Contents
Introduction
If you are working or studying in the field of psychology or market research you will most likely encounter the method of Factor Analysis sooner or later. A useful tool in expolatory analysis, it builds on the concept of variance to find underlying factors in a dataset that make up patterns.
Understanding Factor Analysis
Factor Analysis is a statistical method that uncovers the underlying structure of observed variables, assuming they can be represented by latent factors. A smaller number of latent factors (or unobserved variables) may reflect a big set of observed variables. The goal is to identify and interpret these factors, simplifying complex information and revealing the reasons for variable relationships. Factor Analysis aids dataset interpretation by reducing the number of variables to a fewer set of variables (latent factors). In essence, a large number of variables is efficiently condensed into smaller amount of factors.
Assumptions
Factor Analysis is a linear generative model and assumes several assumptions, such as a linear relationship with correlation between variables and factors. There are certain additional assumptions that must be fufilled in a dataset:
- There are no outliers in data.
- There should not be perfect multicollinearity.
- There should not be homoscedasticity between the variables.
Types of Factor Analyses
There are two main types of Factor Analysis: Exploratory Factor Analysis (EFA), which uncovers underlying structures without preconceived notions, and Confirmatory Factor Analysis (CFA), which confirms pre-established hypotheses about factor structure.
Main components
Factor loadings
The relationship of the factor and directly observed variables is described by the factor loadings. They can be interpreted like correlation coefficients and indicate the strength of the relationship. Like correlation coefficients, the values range from -1 (negative relationship) to 1 (positive relationship). A strong relationship (the closer to -1 or 1, the stronger the relationship) in this case means that a factor explains a lot of the variance in the observed variable. To determine if they are relevant, they are measured against a pre-set threshold. They can be represented as a matrix, which shows the relationship of each observed variable to the factor.
Eigenvalues
It is sometimes also called "characteristic roots". The eigenvalue of factor A tells us how much of the total variance is explained only by this factor. If the first factor explains 60% of the total variance, 40% of the variance has to be explained by the other factor(s). Higher eigenvalues indicate more important factors that capture significant portions of the variability in the observed variables. Remember, our aim is to find just the most important factors, which explain a maximum possible amount of variance.
Communalities
Represents the proportion of variance in each variable accounted for by the factors that were identified in the Factor Analysis. Higher communalities (close to 1) indicate that the factor model accounts well for the variance in the observed variables.
Uniqueness
Represents the proportion of variance in each variable not explained by the factors. Lower uniqueness values suggest that a larger proportion of the variable's variance is accounted for by the factors.
Step by step guide
In the following, important concepts of Factor Analysis are explained along with the implementation in Python.
Step 1: Determining the number of Factors
There are different approaches of deciding how many factors are ideal. One is the Kaiser Criterion. This decision rule says that, if the eigenvalue is larger than 1, the factor is considered; and if it is below 1, it can be excluded. You can also take a graphical approach and determine the number of factors using a scree plot.
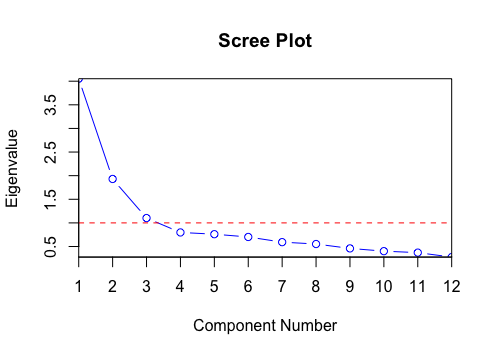
Looking at the plot (Figure 1), you may notice the elbow of the curve (the point, where the curve visibly bends; in this case, from steep to moderate slope). Another way to understand where this point lies is to take the name of this plot literally. If you imagine scree sliding down the curve, the cutoff is made at the point where the scree will stop sliding down the mountain. All factors that lie above this point are considered as factors, all points below the cutoff are not considered. In the given plot, you would include only the first two factors.
The first step, after of course having prepared your dataset df, is to extract the factors using an appropriate technique (e.g., PCA, maximum likelihood) based on assumptions and research objectives. This is however beyond the scope of this Wiki article. We can then determine the number of factors that we want to retain using the methods listed above.
# Import necessary libraries
import pandas as pd
from sklearn.datasets import load_iris
from factor_analyzer import FactorAnalyzer
import matplotlib.pyplot as plt
# Create scree plot using matplotlib
plt.scatter(range(1,df.shape[1]+1),ev)
plt.plot(range(1,df.shape[1]+1),ev)
plt.title('Scree Plot')
plt.xlabel('Factors')
plt.ylabel('Eigenvalue')
plt.grid()
plt.show() # Figure 2
!! Figure 2
Step 2: Fitting the model
In the following snippet of code we fit the model to our data, using 2 factors (as defined by looking at the scree plot - Figure 2). Here, we use maximum likelohood to extract the factors. There are different methods to do this based on the assumptions and research objectives. This is however beyond the scope of this Wiki article.
# Initialize FactorAnalyzer with the desired number of factors
num_factors = 2
factor_model = FactorAnalyzer(n_factors=num_factors, method='ml') # 'ml' stands for maximum likelihood
# Fit the model to the data
factor_model.fit(data)
# Extract factor loadings
loadings = factor_model.loadings_
# Display factor loadings
loadings_df = pd.DataFrame(loadings, index=data.columns,
columns=[f'Factor {i+1}' for i in range(num_factors)])
An additional step is factor rotation, which helps in visualization and interpretation of the factors, however, does not influence the obtained results. Since this Wiki article only aims to give a short overview over the method of Factor Analysis, it is not included in this guide. Futher Python examples of factor rotation can be find here.
Factor Analysis vs. Principal Component Analysis (PCA)
You may have noticed that Factor Analysis reminds you of Principal Component Analysis (PCA). Both Factor Analysis and PCA are data reduction techniques. While they are similar in principle, the two methods have a few fundamental differences. PCA focuses on capturing maximum variance in data through uncorrelated components. In contrast, Factor Analysis aims to unveil underlying factors that influence observed variables, emphasizing interpretability. Factor Analysis assumes correlations among variables stem from common factors, offering insights into the true structure. Simply put, PCA is a linear combination of variables while Factor Analysis is a measurement model of a latent variable. A more thorough comparison and explanation can be found here.
The author of this entry is Hannah Heyne.