Difference between revisions of "Linear Regression in Python"
| (2 intermediate revisions by one other user not shown) | |||
| Line 13: | Line 13: | ||
This involves predicting a dependent variable based on a single independent variable. The equation of the regression line is given by: | This involves predicting a dependent variable based on a single independent variable. The equation of the regression line is given by: | ||
| − | + | [[File:lin_regr_form1.png|300px|center]] | |
| − | where y - the dependent variable, x - the independent variable, m/ | + | where y - the dependent variable, x - the independent variable, m/b<sub>1</sub> - the slope of the line (represents the change in y for a unit change in x), and b/b<sub>0</sub>x - the intercept (the value of y when x is 0). |
===2. Multiple linear regression=== | ===2. Multiple linear regression=== | ||
| − | This involves predicting a dependent variable, that can be explained by multiple independent variables < | + | This involves predicting a dependent variable, that can be explained by multiple independent variables (x<sub>1</sub>, x<sub>2</sub>, ..., x<sub>n</sub>). In this case the equation is extended to: |
| − | + | [[File:lin_regr_form2.png|400px|center]] | |
| − | where, y - the dependent variable, | + | where, y - the dependent variable, x<sub>1</sub>, x<sub>2</sub>, ..., x<sub>n</sub> - the independent variables, b<sub>0</sub> - the intercept, b<sub>1</sub>, b<sub>2</sub>, ... , b<sub>n</sub> - the coefficients that represent the change in y for a unit change in each respective independent variable. |
| − | It is a common practice to denote the outputs with <syntaxhighlight lang="text" inline>y</syntaxhighlight> and the inputs with <syntaxhighlight lang="text" inline>x</syntaxhighlight>. If there are two or more independent variables, then they can be represented as the vector | + | It is a common practice to denote the outputs with <syntaxhighlight lang="text" inline>y</syntaxhighlight> and the inputs with <syntaxhighlight lang="text" inline>x</syntaxhighlight>. If there are two or more independent variables, then they can be represented as the vector x=(x<sub>0</sub>,...x<sub>n</sub>), where n is the number of inputs. |
| − | Linear regression is among the simplest regression methods. One of its main advantages is the ease of results` interpretation. Let us consider a scenario, where we | + | Linear regression is among the simplest regression methods. One of its main advantages is the ease of results` interpretation. Let us consider a scenario, where we need to determine the linear relationship between the weight of a dog and age in months. ''Are we able to estimate the weight of a dog, if we are given the age in months?'' |
| − | ==Linear regression | + | ==Linear regression implementation in Python== |
First of all, we will generate synthetic data, representing the relationship between dog ages and weights, using linear regression from scikit-learn to model this relationship and visualize the original data points along with the linear regression line, using matplotlib. | First of all, we will generate synthetic data, representing the relationship between dog ages and weights, using linear regression from scikit-learn to model this relationship and visualize the original data points along with the linear regression line, using matplotlib. | ||
| Line 64: | Line 64: | ||
df = pd.read_csv('your_dataset.csv') | df = pd.read_csv('your_dataset.csv') | ||
| − | # | + | # extract the 'Age' and 'Weight' columns` values from the DataFrame |
ages = df['Age'].values | ages = df['Age'].values | ||
weights = df['Weight'].values | weights = df['Weight'].values | ||
| Line 72: | Line 72: | ||
<syntaxhighlight lang="Python" line> | <syntaxhighlight lang="Python" line> | ||
| − | # | + | # convert the generated data into a pandas DataFrame. |
df = pd.DataFrame({'Age': ages, 'Weight': weights}) | df = pd.DataFrame({'Age': ages, 'Weight': weights}) | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | The generated data, representing dog ages (<syntaxhighlight lang="Python" inline>ages</syntaxhighlight>) and corresponding weights (<syntaxhighlight lang="Python" inline>weights</syntaxhighlight>), is organized into a pandas DataFrame (<syntaxhighlight lang="Python" inline>df</syntaxhighlight>). The | + | The generated data, representing dog ages (<syntaxhighlight lang="Python" inline>ages</syntaxhighlight>) and corresponding weights (<syntaxhighlight lang="Python" inline>weights</syntaxhighlight>), is organized into a pandas DataFrame (<syntaxhighlight lang="Python" inline>df</syntaxhighlight>). The <syntaxhighlight lang="Python" inline>pd.DataFrame</syntaxhighlight> method creates a tabular data structure with labeled columns (''Age'' and ''Weight''). This step is beneficial, because pandas DataFrames provide a convenient way to organize, analyze, and manipulate structured data. The DataFrame structure allows for easy exploration and manipulation of the data via various [https://sustainabilitymethods.org/index.php/Introduction_to_Pandas pandas methods]. |
===4. Display information about the DataFrame=== | ===4. Display information about the DataFrame=== | ||
| Line 90: | Line 90: | ||
===5. Reshape the data=== | ===5. Reshape the data=== | ||
<syntaxhighlight lang="Python" line> | <syntaxhighlight lang="Python" line> | ||
| − | # | + | # reshape the data |
ages_reshaped = df['Age'].values.reshape(-1, 1) | ages_reshaped = df['Age'].values.reshape(-1, 1) | ||
| + | |||
# ages_reshaped = ages.reshape(-1, 1) | # ages_reshaped = ages.reshape(-1, 1) | ||
| − | |||
weights = df['Weight'].values | weights = df['Weight'].values | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Line 112: | Line 112: | ||
<syntaxhighlight lang="Python" line> | <syntaxhighlight lang="Python" line> | ||
| − | # | + | # create an instance of the LinearRegression class |
model = LinearRegression() | model = LinearRegression() | ||
| − | # | + | # train the model on the training set |
model.fit(X_train, y_train) | model.fit(X_train, y_train) | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Line 122: | Line 122: | ||
<syntaxhighlight lang="Python" line> | <syntaxhighlight lang="Python" line> | ||
| − | # | + | # get coefficients and intercept |
coefficients = model.coef_ | coefficients = model.coef_ | ||
intercept = model.intercept_ | intercept = model.intercept_ | ||
| − | # | + | # print coefficients and intercept |
print(f'\nCoefficients: {coefficients}') # Out: Coefficients: [0.49967695] | print(f'\nCoefficients: {coefficients}') # Out: Coefficients: [0.49967695] | ||
print(f'Intercept: {intercept}') # Out: Intercept: 10.731323827720102 | print(f'Intercept: {intercept}') # Out: Intercept: 10.731323827720102 | ||
| Line 142: | Line 142: | ||
<syntaxhighlight lang="Python" line> | <syntaxhighlight lang="Python" line> | ||
| − | # | + | # calculate Mean Squarred Error (MSE) |
mse = mean_squared_error(y_test, y_pred) | mse = mean_squared_error(y_test, y_pred) | ||
print(f'Mean Squared Error: {mse}') # Out: Mean Squared Error: 21.32477052321913 | print(f'Mean Squared Error: {mse}') # Out: Mean Squared Error: 21.32477052321913 | ||
| − | # | + | # calculate Mean Absolute Error (MAE) |
mae = mean_absolute_error(y_test, y_pred) | mae = mean_absolute_error(y_test, y_pred) | ||
print(f'Mean Absolute Error: {mae}') # Out: Mean Absolute Error: 3.9370489509407145 | print(f'Mean Absolute Error: {mae}') # Out: Mean Absolute Error: 3.9370489509407145 | ||
| − | # | + | # calculate Root Mean Squared Error (RMSE) |
rmse = np.sqrt(mse) | rmse = np.sqrt(mse) | ||
print(f'Root Mean Squared Error: {rmse}') # Out: Root Mean Squared Error: 4.617875109097162 | print(f'Root Mean Squared Error: {rmse}') # Out: Root Mean Squared Error: 4.617875109097162 | ||
| Line 190: | Line 190: | ||
==Summary== | ==Summary== | ||
| − | The goal of linear regression is to find the values of the coefficients (m, b in simple linear regression, and | + | The goal of linear regression is to find the values of the coefficients (m, b in simple linear regression, and b<sub>0</sub>, b<sub>1</sub>, ... , b<sub>n</sub> in multiple linear regression) that fit best the observed data, minimizing the difference between the predicted values and the actual values. Linear regression is widely used in various fields for modeling and predicting relationships between variables. Despite linear regression is a powerful and interpretable tool, it may not be suitable for all types of data and relationships. Consideration of its assumptions and potential challenges is essential for the successful application. |
==References== | ==References== | ||
| Line 203: | Line 203: | ||
The author of this entry is Vignesh Mallya. Edited by Evgeniya Zakharova. | The author of this entry is Vignesh Mallya. Edited by Evgeniya Zakharova. | ||
| − | |||
| − | |||
| − | |||
Latest revision as of 12:33, 3 September 2024
THIS ARTICLE IS STILL IN EDITING MODE
Contents
- 1 Introduction
- 2 Types of linear regression
-
3 Linear regression implementation in Python
- 3.1 1. Import necessary libraries
- 3.2 2. Generate / Import data
- 3.3 3. Create a pandas DataFrame from the generated data
- 3.4 4. Display information about the DataFrame
- 3.5 5. Reshape the data
- 3.6 6. Split the data into training and testing sets
- 3.7 7. Create and fit the linear regression model
- 3.8 8. Make predictions on the test set
- 3.9 9. Evaluate the model
- 3.10 10. Plot the results
- 4 Advantages of linear regression
- 5 Disadvantages of linear regression
- 6 Summary
- 7 References
Introduction
Linear regression is a statistical method that is used to predict a continuous dependent variable (also response or output) based on one or more independent variables (also predictors, inputs or regressors). This technique assumes a linear relationship between the dependent and independent variables, which implies that the dependent variable changes proportionally with changes in the independent variables. In other words, there is a function that maps some features or variables to others sufficiently well.
Regression problems usually have one continuous and unbounded dependent variable. The inputs, however, can be continuous, discrete, or even categorical data, such as gender, nationality, or brand.
Types of linear regression
1. Simple linear regression
This involves predicting a dependent variable based on a single independent variable. The equation of the regression line is given by:
where y - the dependent variable, x - the independent variable, m/b1 - the slope of the line (represents the change in y for a unit change in x), and b/b0x - the intercept (the value of y when x is 0).
2. Multiple linear regression
This involves predicting a dependent variable, that can be explained by multiple independent variables (x1, x2, ..., xn). In this case the equation is extended to:
where, y - the dependent variable, x1, x2, ..., xn - the independent variables, b0 - the intercept, b1, b2, ... , bn - the coefficients that represent the change in y for a unit change in each respective independent variable.
It is a common practice to denote the outputs with y and the inputs with x. If there are two or more independent variables, then they can be represented as the vector x=(x0,...xn), where n is the number of inputs.
Linear regression is among the simplest regression methods. One of its main advantages is the ease of results` interpretation. Let us consider a scenario, where we need to determine the linear relationship between the weight of a dog and age in months. Are we able to estimate the weight of a dog, if we are given the age in months?
Linear regression implementation in Python
First of all, we will generate synthetic data, representing the relationship between dog ages and weights, using linear regression from scikit-learn to model this relationship and visualize the original data points along with the linear regression line, using matplotlib.
There are some basic steps to follow during the linear regression implementation. These steps are more or less general for most of the regression approaches.
1. Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split # to split the dataset into training and testing sets
from sklearn.linear_model import LinearRegression # to perform linear regression
from sklearn.metrics import mean_squared_error, mean_absolute_error # to calculate the error
import pandas as pd
2. Generate / Import data
# ensures reproducibility by fixing the random seed (42 is the seed value). The seed is an integer that serves as the starting point for the random number sequence
np.random.seed(42)
# array of 300 random integers between 0 and 60 (represents dog ages in months)
ages = np.random.randint(0, 60, size=300)
# weights array is generated using a linear relationship with ages array and additional random noise
weights = 10 + 0.5 * ages + np.random.normal(0, 5, size=300)
If you have your own dataset, you can import it with the help of the following code:
df = pd.read_csv('your_dataset.csv')
# extract the 'Age' and 'Weight' columns` values from the DataFrame
ages = df['Age'].values
weights = df['Weight'].values
3. Create a pandas DataFrame from the generated data
# convert the generated data into a pandas DataFrame.
df = pd.DataFrame({'Age': ages, 'Weight': weights})
The generated data, representing dog ages (ages) and corresponding weights (weights), is organized into a pandas DataFrame (df). The pd.DataFrame method creates a tabular data structure with labeled columns (Age and Weight). This step is beneficial, because pandas DataFrames provide a convenient way to organize, analyze, and manipulate structured data. The DataFrame structure allows for easy exploration and manipulation of the data via various pandas methods.
4. Display information about the DataFrame
print("DataFrame Shape:", df.shape)
print("\nDataFrame Head:")
print(df.head())
print("\nDataFrame Description:")
print(df.describe())
5. Reshape the data
# reshape the data
ages_reshaped = df['Age'].values.reshape(-1, 1)
# ages_reshaped = ages.reshape(-1, 1)
weights = df['Weight'].values
The reshape(-1, 1) method is used to transform the one-dimensional array into a two-dimensional array with one column. The -1 argument automatically infers the number of rows based on the array`s length.
6. Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(ages_reshaped, weights, test_size=0.2, random_state=42)
We utilized function train_test_split with parameters test_size=0.2 (20% of the data is for testing and 80% is for training) and random_state=42 (reproducibility in the split).
X_train and X_test are the input features for training and testing, while y_train and y_test are the corresponding target values (labels) for training and testing.
7. Create and fit the linear regression model
# create an instance of the LinearRegression class
model = LinearRegression()
# train the model on the training set
model.fit(X_train, y_train)
Linear regression model finds the best value for the intercept and slope, which results in a line that best fits the data. To retrieve the value of the intercept and slope / coefficients calculated by the linear regression algorithm for our dataset, execute the following script:
# get coefficients and intercept
coefficients = model.coef_
intercept = model.intercept_
# print coefficients and intercept
print(f'\nCoefficients: {coefficients}') # Out: Coefficients: [0.49967695]
print(f'Intercept: {intercept}') # Out: Intercept: 10.731323827720102
8. Make predictions on the test set
y_pred = model.predict(X_test)
9. Evaluate the model
For regression algorithms three evaluation indicators are usually used: Mean Squarred Error (MSE), Mean Absolute Error (MAE), Root Mean Squared Error (RMSE). Execute these functions in order to get information about mentioned errors. The results provide a quantitative measure of how well the model performs on the test set.
# calculate Mean Squarred Error (MSE)
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error: {mse}') # Out: Mean Squared Error: 21.32477052321913
# calculate Mean Absolute Error (MAE)
mae = mean_absolute_error(y_test, y_pred)
print(f'Mean Absolute Error: {mae}') # Out: Mean Absolute Error: 3.9370489509407145
# calculate Root Mean Squared Error (RMSE)
rmse = np.sqrt(mse)
print(f'Root Mean Squared Error: {rmse}') # Out: Root Mean Squared Error: 4.617875109097162
There are many factors that contribute to this inaccuracy, some of which are listed here:
- The features we used may not have had a high enough correlation to the values we were trying to predict.
- We assume that this data has a linear relationship, but this is not the case. Visualisation of the data may help to determine.
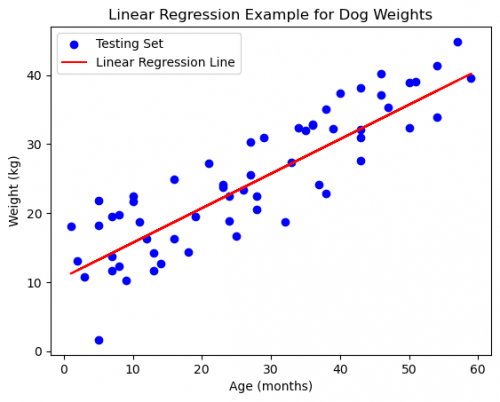
10. Plot the results
plt.scatter(X_test, y_test, label='Testing Set', color='blue') # original data points of test dataset
plt.plot(X_test, y_pred, color='red', label='Linear Regression Line') # linear regression line
plt.xlabel('Age (months)')
plt.ylabel('Weight (kg)')
plt.title('Linear Regression Example for Dog Weights')
plt.legend()
plt.show()
Advantages of linear regression
- Simplicity: Linear regression is straightforward and easy to understand.
- Clear insights: Coefficients provide clear insights into variable relationships.
- Efficiency: Computationally efficient, especially with large datasets.
- Versatility: No strict assumptions about variable distribution.
- Feature selection: Useful for selecting important features.
Disadvantages of linear regression
- Linearity assumption: Effective only for linear relationships.
- Outlier sensitivity: Impactful sensitivity to outliers.
- Assumption challenges: Assumes independence and homoscedasticity.
- Multicollinearity issues: Problems with highly correlated independent variables.
- Categorical data handling: Not ideal for categorical data without adjustments.
- Overfitting/Underfitting: Vulnerable to overfitting or underfitting without regularization.
Summary
The goal of linear regression is to find the values of the coefficients (m, b in simple linear regression, and b0, b1, ... , bn in multiple linear regression) that fit best the observed data, minimizing the difference between the predicted values and the actual values. Linear regression is widely used in various fields for modeling and predicting relationships between variables. Despite linear regression is a powerful and interpretable tool, it may not be suitable for all types of data and relationships. Consideration of its assumptions and potential challenges is essential for the successful application.
References
To learn more about this topic, please refer to the following resources:
1. Real Python (n.d) https://realpython.com/linear-regression-in-python/
2. GeeksforGeeks (n.d) https://www.geeksforgeeks.org/linear-regression-python-implementation/
3. Scikit-learn (n.d) https://scikit-learn.org/stable/modules/classes.html#module-sklearn.linear_model
The author of this entry is Vignesh Mallya. Edited by Evgeniya Zakharova.