Difference between revisions of "Bootstrapping in Python"
(Created page with "THIS ARTICLE IS STILL IN EDITING MODE ==Introduction== The term "bootstrap" is euphonic with the metaphor of pulling oneself up by one's bootstraps, signifying the achieveme...") |
|||
| Line 5: | Line 5: | ||
The term "bootstrap" is euphonic with the metaphor of pulling oneself up by one's bootstraps, signifying the achievement of the seemingly impossible without external assistance. Analogously, as seen in Raspe's tales of Baron Munchausen, who extricated himself and his horse from a swamp by his own hair, the Bootstrap technique enables the attainment of statistical insights independently, bypassing the need for predefined formulas. | The term "bootstrap" is euphonic with the metaphor of pulling oneself up by one's bootstraps, signifying the achievement of the seemingly impossible without external assistance. Analogously, as seen in Raspe's tales of Baron Munchausen, who extricated himself and his horse from a swamp by his own hair, the Bootstrap technique enables the attainment of statistical insights independently, bypassing the need for predefined formulas. | ||
| − | Bootstrap is applicable for any samples. It is useful when: | + | '''Bootstrap is applicable for any samples. It is useful when:''' |
| − | + | ||
| − | + | 1. observations are not described by normal distribution;<br> | |
| + | 2. there are no statistical tests for the desired quantities. | ||
===Theoretical aspect=== | ===Theoretical aspect=== | ||
| Line 17: | Line 18: | ||
[[File:Illustration_bootstrap.png|800px|center|Figure 1. Illustration of bootstrapping method. Source: [https://en.wikipedia.org/wiki/Bootstrapping_(statistics)#/media/File:Illustration_bootstrap.svg Wikipedia]]] | [[File:Illustration_bootstrap.png|800px|center|Figure 1. Illustration of bootstrapping method. Source: [https://en.wikipedia.org/wiki/Bootstrapping_(statistics)#/media/File:Illustration_bootstrap.svg Wikipedia]]] | ||
| − | '''Advantages''': | + | '''Advantages''': |
| − | 1. Simplicity and flexibility. | + | |
| − | 2. No knowledge about data distribution is needed. | + | 1. Simplicity and flexibility. <br> |
| − | 3. Helps to avoids the cost of repeating the experiment to get more data. | + | 2. No knowledge about data distribution is needed. <br> |
| + | 3. Helps to avoids the cost of repeating the experiment to get more data. <br> | ||
4. Usually provides a more accurate estimates of a statistic than "standard" methods utilizing normal distribution. | 4. Usually provides a more accurate estimates of a statistic than "standard" methods utilizing normal distribution. | ||
| − | '''Disadvantages''': | + | '''Disadvantages''': |
| − | 1. Computational intensity. The process involves resampling from the dataset multiple times, which might be time-consuming for extensive datasets. | + | |
| − | 2. Dependence on the original data. Bootstrapping assumes that the original dataset is representative of the population. | + | 1. Computational intensity. The process involves resampling from the dataset multiple times, which might be time-consuming for extensive datasets. <br> |
| + | 2. Dependence on the original data. Bootstrapping assumes that the original dataset is representative of the population. <br> | ||
3. Sensitivity to outliers. Since bootstrap samples with replacement, outliers may be overrepresented in the resampled datasets, affecting the stability of the results. | 3. Sensitivity to outliers. Since bootstrap samples with replacement, outliers may be overrepresented in the resampled datasets, affecting the stability of the results. | ||
| Line 77: | Line 80: | ||
<syntaxhighlight lang="Python" line> | <syntaxhighlight lang="Python" line> | ||
# upper 0.99 quantile lies in this interval with 95% confidence | # upper 0.99 quantile lies in this interval with 95% confidence | ||
| − | print(f'{upper_quantiles.quantile(0.025):.2f}') | + | print(f'{upper_quantiles.quantile(0.025):.2f}') # Out: 94.89 |
| − | print(f'{upper_quantiles.quantile(0.975):.2f}') | + | print(f'{upper_quantiles.quantile(0.975):.2f}') # Out: 98.69 |
| − | + | ||
| − | |||
| − | 98.69 | ||
| − | |||
# lower 0.01 quantile lies in this interval with 95% confidence | # lower 0.01 quantile lies in this interval with 95% confidence | ||
| − | print(f'{lower_quantiles.quantile(0.025):.2f}') | + | print(f'{lower_quantiles.quantile(0.025):.2f}') # Out: 0.55 |
| − | print(f'{lower_quantiles.quantile(0.975):.2f}') | + | print(f'{lower_quantiles.quantile(0.975):.2f}') # Out: 4.62 |
</syntaxhighlight> | </syntaxhighlight> | ||
| − | |||
| − | |||
===Example 2. Bootstrapping as an alternative to t-test=== | ===Example 2. Bootstrapping as an alternative to t-test=== | ||
| Line 116: | Line 114: | ||
<syntaxhighlight lang="Python" line> | <syntaxhighlight lang="Python" line> | ||
AB_difference = samples_B.mean() - samples_A.mean() | AB_difference = samples_B.mean() - samples_A.mean() | ||
| − | print(f"Difference of mean values {AB_difference:.2f}") | + | print(f"Difference of mean values {AB_difference:.2f}") # Out: Difference of mean values 1.63 |
</syntaxhighlight> | </syntaxhighlight> | ||
| − | |||
This is a rather small difference, considering all values are close to 100. Let's calculate the probability that we observe such a difference only by chance. To do that, we concatenate two samples and run bootstrap simulation as follows: | This is a rather small difference, considering all values are close to 100. Let's calculate the probability that we observe such a difference only by chance. To do that, we concatenate two samples and run bootstrap simulation as follows: | ||
| − | 1. Divide the united sample into 2 equal subsamples. | + | 1. Divide the united sample into 2 equal subsamples. <br> |
| − | 2. Calculate the difference of means between 2 subsamples. | + | 2. Calculate the difference of means between 2 subsamples. <br> |
3. Increment the counter, when the observed bootstrap mean difference is greater than that we calculated for initial samples. ''If that happens often, it is very probable that our initial difference is just accidental, and the means of our samples are close''. | 3. Increment the counter, when the observed bootstrap mean difference is greater than that we calculated for initial samples. ''If that happens often, it is very probable that our initial difference is just accidental, and the means of our samples are close''. | ||
| − | Repeat these steps 1000 times. By running bootstrap, we find a probability that in "random" subsamples difference of means is equal to or greater than in our initial samples. That is basically the p-value for the following hypothesis | + | Repeat these steps 1000 times. By running bootstrap, we find a probability that in "random" subsamples difference of means is equal to or greater than in our initial samples. That is basically the p-value for the following hypothesis H<sub>0</sub>: mean values between 2 samples are the same. |
<syntaxhighlight lang="Python" line> | <syntaxhighlight lang="Python" line> | ||
| Line 160: | Line 157: | ||
else: | else: | ||
print("Accept H0: mean values are the same") | print("Accept H0: mean values are the same") | ||
| + | |||
| + | # Out: p-value = 0.042 | ||
| + | # Out: Reject H0: mean values are different | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| Line 173: | Line 173: | ||
plt.show() | plt.show() | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| + | |||
| + | [[File:bootstr_2example4.png|500px]] | ||
From the figure we conclude that value of 1.63 is quite rarely encountered in the simulation, making it unlikely that such a value for the initial samples is acquired by chance. | From the figure we conclude that value of 1.63 is quite rarely encountered in the simulation, making it unlikely that such a value for the initial samples is acquired by chance. | ||
| Line 179: | Line 181: | ||
<syntaxhighlight lang="Python" line> | <syntaxhighlight lang="Python" line> | ||
ttest_ind(samples_A.values, samples_B.values) | ttest_ind(samples_A.values, samples_B.values) | ||
| + | # Out: TtestResult(statistic=-1.7971305016442471, pvalue=0.07790788332728987, df=54.0)Out: TtestResult(statistic=-1.7971305016442471, pvalue=0.07790788332728987, df=54.0) | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | |||
The result is the similar, p-value is very small, the means differ significantly. However, t-test is much more "sure" about the results, while the p-value for bootstrapping was barely below threshold. | The result is the similar, p-value is very small, the means differ significantly. However, t-test is much more "sure" about the results, while the p-value for bootstrapping was barely below threshold. | ||
| Line 187: | Line 189: | ||
1. https://medium.com/analytics-vidhya/what-is-bootstrapping-in-machine-learning-777fc44e222a (a simple article, also contains a link to the original article) | 1. https://medium.com/analytics-vidhya/what-is-bootstrapping-in-machine-learning-777fc44e222a (a simple article, also contains a link to the original article) | ||
| + | |||
2. https://towardsdatascience.com/an-introduction-to-the-bootstrap-method-58bcb51b4d60 (a more mathematical article explaining why bootstrap actually works, has a lot of further links) | 2. https://towardsdatascience.com/an-introduction-to-the-bootstrap-method-58bcb51b4d60 (a more mathematical article explaining why bootstrap actually works, has a lot of further links) | ||
| + | |||
3. https://en.wikipedia.org/wiki/Bootstrapping_(statistics) | 3. https://en.wikipedia.org/wiki/Bootstrapping_(statistics) | ||
| − | The author of this entry is Igor Kvachenok | + | The author of this entry is Igor Kvachenok. |
| + | |||
| + | [[Category:Statistics]] | ||
| + | [[Category:Python basics]] | ||
Revision as of 13:35, 27 February 2024
THIS ARTICLE IS STILL IN EDITING MODE
Contents
Introduction
The term "bootstrap" is euphonic with the metaphor of pulling oneself up by one's bootstraps, signifying the achievement of the seemingly impossible without external assistance. Analogously, as seen in Raspe's tales of Baron Munchausen, who extricated himself and his horse from a swamp by his own hair, the Bootstrap technique enables the attainment of statistical insights independently, bypassing the need for predefined formulas.
Bootstrap is applicable for any samples. It is useful when:
1. observations are not described by normal distribution;
2. there are no statistical tests for the desired quantities.
Theoretical aspect
Bootstrapping (sometimes also just bootstrap) is a method for estimating statistical quantities without reliance on explicit formulas.
To derive a specified statistic for a sample (such as the mean or variance, quantile, etc.), using bootstrap, pseudo-samples or subsamples are generated from the original sample by drawing with replacement. The mean (variance, quantile, etc.) is then computed for each pseudo-sample. Theoretically, this process can be repeated multiple times, generating numerous instances of the parameter of interest and allowing for the assessment of its distribution.
Advantages:
1. Simplicity and flexibility.
2. No knowledge about data distribution is needed.
3. Helps to avoids the cost of repeating the experiment to get more data.
4. Usually provides a more accurate estimates of a statistic than "standard" methods utilizing normal distribution.
Disadvantages:
1. Computational intensity. The process involves resampling from the dataset multiple times, which might be time-consuming for extensive datasets.
2. Dependence on the original data. Bootstrapping assumes that the original dataset is representative of the population.
3. Sensitivity to outliers. Since bootstrap samples with replacement, outliers may be overrepresented in the resampled datasets, affecting the stability of the results.
Synthetic examples of bootstrapping
Example 1. Bootstrapping for quantile evaluation
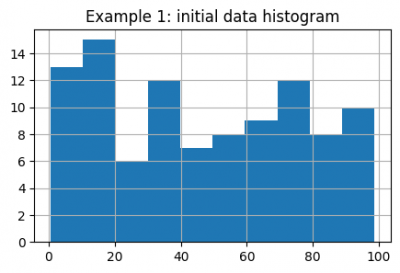
We will generate a sample with some random distribution:
import pandas as pd
import numpy as np
from scipy.stats import ttest_ind
import matplotlib.pyplot as plt
np.random.seed(42)
data = pd.Series(np.random.rand(100) * 100)
data.hist(figsize=(5, 3))
plt.title("Example 1: initial data histogram")
plt.show()
Using bootstrap to evaluate outliers in this case is much more reliable, than calculating normal distribution quantiles. For this purpose we will generate 1000 subsamples using pandas `sample` function and a loop. It is important to set `replace=True`, as bootstrap relies on drawing samples with replacement. We will evaluate the upper 0.99 and lower 0.01 quantiles.
upper_quantiles = []
lower_quantiles = []
for i in range(1000):
subsample = data.sample(frac=1, replace=True)
upper_quantiles.append(subsample.quantile(0.99))
lower_quantiles.append(subsample.quantile(0.01))
upper_quantiles = pd.Series(upper_quantiles)
lower_quantiles = pd.Series(lower_quantiles)
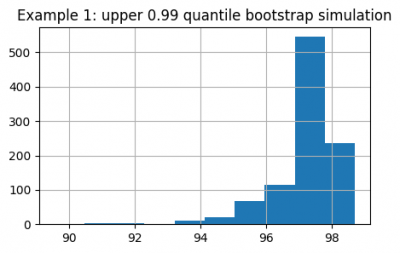
We get an experimental distribution for both quantiles:
upper_quantiles.hist(figsize=(5, 3))
plt.title("Example 1: upper 0.99 quantile bootstrap simulation")
plt.show()
Now we can estimate confidence intervals for the upper and lower 0.01 quantiles:
# upper 0.99 quantile lies in this interval with 95% confidence
print(f'{upper_quantiles.quantile(0.025):.2f}') # Out: 94.89
print(f'{upper_quantiles.quantile(0.975):.2f}') # Out: 98.69
# lower 0.01 quantile lies in this interval with 95% confidence
print(f'{lower_quantiles.quantile(0.025):.2f}') # Out: 0.55
print(f'{lower_quantiles.quantile(0.975):.2f}') # Out: 4.62
Example 2. Bootstrapping as an alternative to t-test
Bootstrap can be easily implemented for analyzing difference between mean values of two samples.
# generate 2 samples
samples_A = pd.Series(
[100.24, 97.77, 95.56, 99.49, 101.4 , 105.35, 93.33, 93.02,
101.37, 95.66, 93.34, 100.75, 104.93, 97. , 95.46, 100.03,
102.34, 93.23, 97.05, 97.76, 93.63, 100.32, 99.51, 99.31,
102.41, 100.69, 99.67, 100.99],
name='sample_A')
samples_B = pd.Series(
[101.67, 102.27, 97.01, 103.46, 100.76, 101.19, 99.11, 97.59,
101.01, 101.45, 94.3 , 101.55, 96.33, 99.03, 102.33, 97.32,
93.25, 97.17, 101.1 , 102.57, 104.59, 105.63, 93.93, 103.37,
101.62, 100.62, 102.79, 104.19],
name='sample_B')
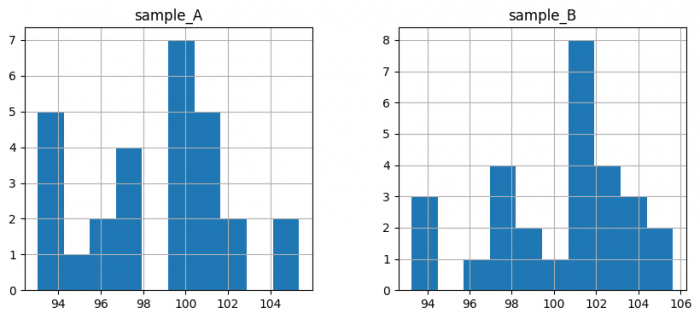
pd.concat([samples_A, samples_B], axis=1).hist(figsize=(10, 4))
plt.show()
AB_difference = samples_B.mean() - samples_A.mean()
print(f"Difference of mean values {AB_difference:.2f}") # Out: Difference of mean values 1.63
This is a rather small difference, considering all values are close to 100. Let's calculate the probability that we observe such a difference only by chance. To do that, we concatenate two samples and run bootstrap simulation as follows:
1. Divide the united sample into 2 equal subsamples.
2. Calculate the difference of means between 2 subsamples.
3. Increment the counter, when the observed bootstrap mean difference is greater than that we calculated for initial samples. If that happens often, it is very probable that our initial difference is just accidental, and the means of our samples are close.
Repeat these steps 1000 times. By running bootstrap, we find a probability that in "random" subsamples difference of means is equal to or greater than in our initial samples. That is basically the p-value for the following hypothesis H0: mean values between 2 samples are the same.
alpha = 0.05
num_samples = 1000
count = 0
diffs = []
united_samples = pd.concat([samples_A, samples_B])
for i in range(num_samples):
subsample = united_samples.sample(frac=1, replace=True)
# create 2 equal subsamples
subsample_A = subsample[:len(samples_A)]
subsample_B = subsample[len(samples_A):]
# calculate difference of means of 2 subsamples
bootstrap_difference = subsample_B.mean() - subsample_A.mean()
diffs.append(bootstrap_difference)
# if the mean difference is bigger
if bootstrap_difference >= AB_difference:
print(bootstrap_difference)
count += 1
# p-value is the rate of cases when
# bootstrap difference was greater than AB_difference
pvalue = 1. * count / num_samples
print('p-value =', pvalue)
if pvalue < alpha:
print("Reject H0: mean values are different")
else:
print("Accept H0: mean values are the same")
# Out: p-value = 0.042
# Out: Reject H0: mean values are different
Thus, we showed using bootstrap, that the difference between mean values of the above samples is statistically significant.
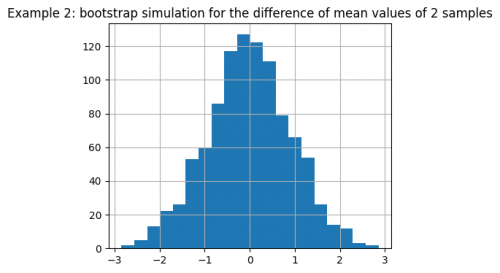
We can also visualize the bootstrap simulation for the difference of mean values:
pd.Series(diffs).hist(bins=20, figsize=(5, 4))
plt.title(
"Example 2: bootstrap simulation for" +
"the difference of mean values of 2 samples")
plt.show()
From the figure we conclude that value of 1.63 is quite rarely encountered in the simulation, making it unlikely that such a value for the initial samples is acquired by chance.
Compare this result to t-test:
ttest_ind(samples_A.values, samples_B.values) # Out: TtestResult(statistic=-1.7971305016442471, pvalue=0.07790788332728987, df=54.0)Out: TtestResult(statistic=-1.7971305016442471, pvalue=0.07790788332728987, df=54.0)
The result is the similar, p-value is very small, the means differ significantly. However, t-test is much more "sure" about the results, while the p-value for bootstrapping was barely below threshold.
Further reading
1. https://medium.com/analytics-vidhya/what-is-bootstrapping-in-machine-learning-777fc44e222a (a simple article, also contains a link to the original article)
2. https://towardsdatascience.com/an-introduction-to-the-bootstrap-method-58bcb51b4d60 (a more mathematical article explaining why bootstrap actually works, has a lot of further links)
3. https://en.wikipedia.org/wiki/Bootstrapping_(statistics)
The author of this entry is Igor Kvachenok.