Multi-Criteria Decision Making in Python
THIS ARTICLE IS STILL IN EDITING MODE
Contents
Introduction
Decision-making processes are part of our everyday life. Some decisions require very little effort and thought. However, there are real-life problems, we would have to evaluate many criteria for making a decision. The situation becomes more difficult when these criteria conflict with each other!
For example, a student needs to consider different criteria to choose a subject for an undergraduate program at a university. These criteria include not only the student’s interest but also prospects, location of the university, size of the study program, etc. But we should consider that each of these criteria would have different importance from our point of view.
Decision Making Process
In general, a decision-making process can be divided into 8 steps as follows:
1. Define the problem: Accurate problem definition is very crucial for effective decision making and all the stakeholders must agree with its definition.
2. Determine requirements: Requirements indicate what conditions must be met for any acceptable solution. If we want to explain it in mathematical form, the constraints describing the set of feasible solutions are considered to be requirements of the decision problem.
3. Establish goals: The goals we define can be inconsistent and conflicting. This is very common in the real world. For this reason, various decision-making methods have been developed.
4. Identify alternatives: As we collect information about our problem, we would identify several possible alternatives which lead us to our desired conditions.
5. Define criteria: In this step, we determine the decision criteria that evaluate and compare our alternatives. Criteria should be chosen to represent the preferences of potential stakeholders. Criteria should have the following features:
* Ability to discriminate between alternatives, * Comprehensive and determined based on our goals, * Non-redundant (independent), * Not be too large in number, just a few!
6. Choose a decision-making tool: To be able to choose the right tool and methods, we must consider the definition of the problem and also the goals of the decision-makers.
7. Evaluate alternatives against criteria: By using the decision-making tool, it is possible to rank the alternatives or get a subset of the possible solutions.
8. Validate solutions against the problem statement: In the last step, we must check whether the chosen options meet the requirements and goals of the decision-making problem.
Multi-Criteria Decision Making
When there is a complex problem and we must evaluate multiple conflicting criteria, multi-criteria decision making (MCDM) as a sub-discipline of operations research, leads us to more informed and better decisions by making the weights and associated trade-offs between the criteria. In general, MCDM is used to reduce the incidence of decision-maker bias as well as the lack of success in group decision-making.
The MCDM is divided into two categories: 1. Multi-attribute decision making (MADM): This category concentrates on problems with discrete decision spaces, ranking the alternatives. In these studies, the set of alternatives has been predetermined.
2. Multi-objective decision making (MODM): In this category, several competing objectives are required to be optimized simultaneously and decision space is continuous.
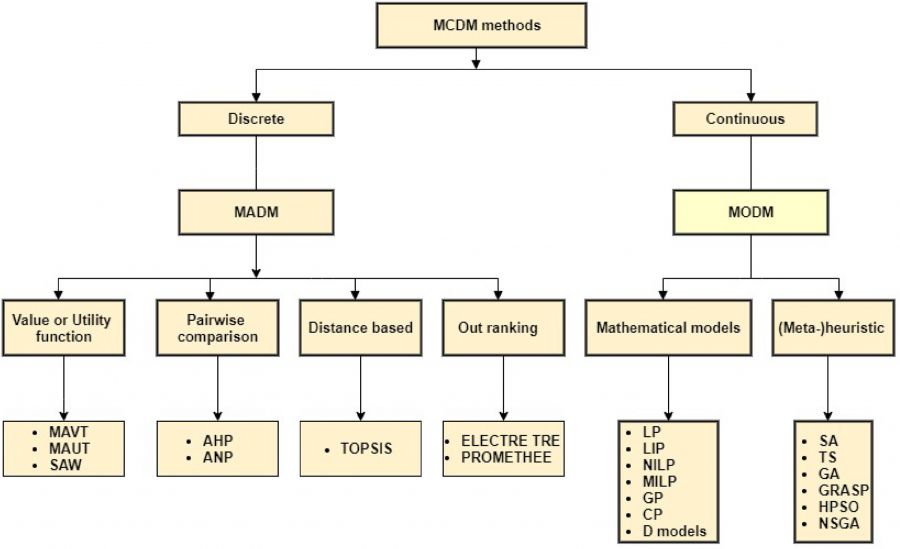
Figure (1) below shows the classification of MCDM methods:
Figure (1). MAV(U)T: multi-attribute value(utility) theory; SAW: simple additive weighting; AHP/ANP: Analytical hierarchy(network) process; TOPSIS: a technique for order of preference by similarity to ideal solution; ELECTRE TRE: elimination and choice expressing reality; PROMETHEE: preference ranking organization method for enrichment evaluation; LP: linear programming; ILP: integer linear programming; NILP: non-integer linear programming; MILP: mixed integer linear programming; GP: goal programming; CP: compromise programming; D_models: dynamic models; SA: simulating annealing; TS: tabu search; GRASP: greedy randomized adaptive search procedure; HPSO: hybrid particle swarm optimization; NSGA: non-dominated sorted genetic algorithm
Example
In this part, we want to solve a MADM problem. Suppose you want to enroll in a fitness center. There are 4 centers in your city (A, B, C, D). The criteria that influence your decision are as follows:
Opening hours(hours/day) Location (Distance from your home (km)) Equipment (Basic: 1, Intermediate:2, Advanced:3) Membership fee(fee/month) Cleanliness (Excellent:4, Good:3, Sufficient:2, Inadequate:1)
The weight of each criterion is also as follows:
Opening hours weight: 0.15 Location weight: 0.2 Equipment weight: 0.35 Membership fee weight: (0.1 Cleanliness weight: 0.2 We can create the decision matrix with pandas and specify the score/rate of each criterion for each alternative.
# Create a Pandas DataFrame from a Numpy array and specify the index column and column headers
# import required libraries
import numpy as np
import pandas as pd
# creating a numpy array (score of each criterion)
rate = np.array([[24, 5, 2, 20, 3],
[12, 2, 1, 13, 2],
[6, 3, 2, 15, 2],
[12, 7, 3, 19, 4]])
# generating the Pandas data frame
decision_matrix = pd.DataFrame(data = rate,
index = ["A", "B", "C", "D"],
columns = ["opening_hours",
"location", "equipment", "membership_fee","cleanliness"])
# printing the data frame
print(decision_matrix)
#Importance of each criterion
import plotly.express as px
import pandas as pd
weights=[0.15, 0.2,0.35,0.1 ,0.2]
df = pd.DataFrame(dict(
w_vector=weights,
criteria=['Opening hours','Location','Equipment','Membership Fee','Cleanliness']))
fig = px.line_polar(df, r='w_vector', theta='criteria', line_close=True,
title="Importance of Each Criterion")
fig.update_traces(fill='toself')
fig.show()
This code produces a polar plot showing the different weighting of the criteria. First, the weights are defined. Then, a dictionary with the two keys "w_vector" and "criteria" are created within a pandas data frame. This information is then used to create the polar plot, whereas r stands for radius and describes the distance of the line between the center and the outer boundary and theta divides the circle into five equal parts to depict each criterion.
The next step is applying a MADA method. We implement the Simple Additive Weighting (SAW) method for this problem. The basic concept of the SAW method is to find the weighted sum of ratings on each alternative on all attributes.
In this example, opening hours, equipment, and cleanliness are benefit criteria while location and membership fee are cost criteria. A benefit criterion means that the higher an alternative scores in terms of it, the better the alternative is. The opposite is considered true for the cost criteria.
All criteria must be either benefit or cost criteria in order to use the SAW method. For this reason, we reverse the values of membership fee and location.
decision_matrix['location'] = 1/decision_matrix['location']
decision_matrix['membership_fee']= 1/decision_matrix['membership_fee']
decision_matrix
The SAW method requires the process of normalizing the decision matrix. We use Max-Min techniques.
# Normalization is a process for rescaling the real values of a numeric attribute into a range from 0 to 1
from sklearn.preprocessing import normalize
decision_matrix_norm = normalize(decision_matrix, axis=0, norm='max')
decision_matrix_norm
The final result is obtained from ranking the sum of the normalized matrix multiplication by the weights:
result = np.dot(weights,decision_matrix_norm.transpose())
result_index = pd.DataFrame(data = result,
index = ["A", "B", "C", "D"],
columns = ["value"])
result_sorted = result_index.sort_values(by=['value'], ascending = False)
result_sorted
The np.dot command multiplies matrices, in our case the two-dimensional matrix of the normalized values with the 1-dimensional matrix of the weights. The matrix of the normalized values also needed to be transposed so that the number of rows and columns of the two matrices are the same and can be multiplied. Then, we gave names to the rows ("index") and the column ("value") and sorted them by the values in ascending order. We can also plot this with the following code:
result_sorted['value'].plot(kind='bar', xlabel='Fitness Center', ylabel= 'Value',rot=0,colormap='coolwarm')
In this example, alternative D has the highest value.
We can also solve the above example with the "mcdm" package. The package can be installed from "PyPI" or from its "GitHub" repository. This package includes the different methods of scoring, weighting, correlation, and normalization.
import mcdm
alt_names = ["A", "B", "C", "D"]
mcdm.rank(decision_matrix_norm, alt_names=alt_names, w_vector= weights, s_method="SAW")
The result shows that Fitness Center D has the highest value.
Advantages & Limitations
A well-designed MCDM provides an appropriate and cost-effective way for reducing a large number of options. It also increases transparency in decision-making. In this method, we can use both quantitative and qualitative evaluation criteria. However, if there are diverse alternatives, it would be difficult to find the same criteria that can evaluate all of these alternatives. Moreover, since the choice of criteria and scoring sometimes requires judgment by experts and decision-makers, this judgment is subject to bias, which can reduce the quality of decision-making.
References
Aytekin, Ahmet. "Comparative analysis of the normalization techniques in the context of MCDM problems." Decision Making: Applications in Management and Engineering 4.2 (2021): 1-25. Available online: https://pypi.org/project/mcdm/
Černevičienė, Jurgita, and Audrius Kabašinskas. "Review of multi-criteria decision-making methods in finance using explainable artificial intelligence." Frontiers in artificial intelligence 5 (2022).
Fülöp, János. "Introduction to decision making methods." BDEI-3 Workshop, Washington . 2005 Available online: https://www.1000minds.com/decision-making/what-is-mcdm-mcda
Gebre, Sintayehu Legesse, et al. "Multi-criteria decision making methods to address rural land allocation problems: A systematic review." International Soil and Water Conservation Research 9.4 (2021): 490-501.
Kazimieras Zavadskas, Edmundas, Jurgita Antucheviciene, and Samarjit Kar. "Multi-objective and multi-attribute optimization for sustainable development decision aiding." Sustainability 11.11 (2019): 3069.
Montibeller, Gilberto, and Detlof von Winterfeldt. "Biases and debiasing in multi-criteria decision analysis." 2015 48th Hawaii International Conference on System Sciences. IEEE, 2015.
Triantaphyllou, Evangelos, et al. "Multi-criteria decision making: an operations research approach." Encyclopedia of electrical and electronics engineering 15.1998 (1998): 175-186.
The author of this entry is XX. Edited by Milan Maushart