Model evaluation metrics (binary classification)

THIS ARTICLE IS STILL IN EDITING MODE

Introduction

This entry reflects the process how to manage the model in order to predict a binary variable, including methods and metrics for its evaluation. We will focus on binary classification, confusion matrix, Receiver Operating Characteristics (ROC), and Area Under Curve (AUC).

Binary classification with Decision tree

import pandas as pd
import matplotlib.pyplot as plt

# for model
from sklearn import tree
from sklearn.neural_network import MLPRegressor
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split

# for metrics and scores
from sklearn import metrics
from sklearn.metrics import confusion_matrix
from sklearn.metrics import *

We will use 'Smoke detection' dataset from Kaggle for our examples. It has only numerical features and a dependent variable 'Fire Alarm', which has values [0,1] and can be predicted by the characteristics of the environment, such as Temperature, Humidity, etc. For more information about the dataset, please, refer the "Data card" tab. It is also recommended to do the data inspection before you create any model.

data = pd.read_csv("smoke_detection.csv",sep=',',index_col=0)
pd.set_option('display.max_columns', None)

We will take only a part of all samples for the model. Parameter replace=False at method sample insures the diversity of samples (no row will be taken more than one time).

data_1000 = data.sample(n=1000, replace=False)

For the first case let us create a Decision Tree Classifier with Temperature, Humidity and eCO2 (CO₂ equivalent concentration) as independent variables. Follow the steps below to make the predictions.

First, the selected samples will be split on train and test datasets. train_test_split() from sklearn is one of the most used functions for this task. The independent and dependent variables are necessary to call the function, however, other arguments can be added, for instance, test_size or train_size, which show the percentage of the splitting. We will continue with the default settings of 25% for the test size. The returns are in a special order.

x_train, x_test, y_train, y_test = train_test_split(data_1000.loc[:,['Temperature[C]','Humidity[%]','eCO2[ppm]']],data_1000.loc[:,['Fire Alarm']])

Decision Tree Classifier from scikit-learn automatically decides the thresholds and defines the decision path. Method fit() builds the Decision Tree on the train data. After we created the model and fitted train input and target, we predict the outcome of the test data via the method predict(). More on Decision Trees in Python here.

model= tree.DecisionTreeClassifier()
model.fit(x_train, y_train)
predictions = model.predict(x_test)

Confusion matrix

As the predictions are calculated, the phase of model evaluation can be started.

Let us formulate the confusion matrix, which is a simple evaluation method for the (binary) classification. It reflects the performance of the model on test data by displaying number of correct and wrong predictions for each class with respect to their target values. As the current case is a binary classification the dimension of a matrix is 2x2.

Confusion Matrix		Actual values
Confusion Matrix		Yes (1)	No (0)
Predicted values	Yes (1)	True Positive (TP)	False Positive (FP)
Predicted values	No (0)	False Negative (FN)	True Negative (TN)

confusion_matrix() function takes test`s target true values and predictions as arguments and returns the matrix, however, the matrix by scikit-learn looks differently:

TN	FP
FN	TP

cm = confusion_matrix(y_test, predictions)
print(cm)

[[ 58 13]
[ 10 169]]

Based on the resulted confusion matrix we have:

169 True Positive (TP): The model predicted a positive outcome and it is correct.
13 False Positive (FP): The model predicted a positive outcome and it is wrong (Type I error).
10 False Negative (FN): The model predicted a negative outcome and it is wrong (Type II error).
58 True Negative (TN): The model predicted a negative outcome and it is correct.

True or False define the correctness of the model, regardless the class. Positive or Negative define, in turn, the class, predicted by the model.

Evaluation metrics

The confusion matrix helps to compute the metrics of the model evaluation, namely accuracy, precision and recall. The formulas and their functions in Python are shown below. sklearn.metrics calculates the scores automaticaly.

Accuracy reflects the model performance, by calculating the ratio between correctly predicted outcomes and the whole number of test data samples. True Positive and True Negative are correct predictions. Use the next formula to compute accuracy:

Accuracy = (TP + TN)/(TP + TN + FP + FN) = (169 + 58)/(169 + 58 + 13 + 10) = 0.91

accuracy = accuracy_score(y_test, predictions)
print(f"Accuracy: {accuracy:.2f}") # Out: Accuracy: 0.91

After that it is easy to compute Error rate of the model, which is 1 - Accuracy (ratio of incorrect outcomes).

Recall (sencitivity) determines, how many of actual positive samples from the test data are correctly predicted (that is why it is also called true positive rate). At the matrix actual positive samples are a combination of correcly predicted as positive (TP) and wrongly predicted as negative (FN) outcomes:

Recall = TP/(TP + FN) = 169/(169 + 10) = 0.94

recall = recall_score(y_test, predictions)
print(f"Recall: {recall:.2f}") # Out: Recall: 0.94

Another metric to compute is Precision, which describes, how accurate the model is in positive prediction, namely, the ratio of true positive predictions to a number of all samples, defined as positive:

Precision = TP/(TP + FP) = 169/(169 + 13) = 0.93

precision = precision_score(y_test, predictions)
print(f"Precision: {precision:.2f}") # Out: Precision: 0.93

F-measure or F1-score is a harmonic mean between recall and precision, which value is in a range between 0 and 1. The goal of the model is to minimize false positive and false negative outcomes, therefore, the F-measure closed to 1 reflects a high model performance.

F-measure = (2\*Precision\*Recall)/(Precision + Recall) = 2TP/(2TP + FP + FN) = 169/(169 + 13 + 10) = 0.94

f_measure = f1_score(y_test, predictions)
print(f"F-measure: {f_measure:.2f}") # Out: F1-score: 0.94

It is also possible to calculate how often the model fails to predict correct instances, by computing Type I and Type II Errors.

In addition, with the help of confusion matrix we can make a decision about the Null hypothesis (Hypothesis testing).

Confusion Matrix		Null hypothesis H0 is
Confusion Matrix		True	False
decision about H0	fail to reject	TN	FN (II type error - you accept H0, when H0 is false)
decision about H0	reject H0	FP (I type error. H0 - true, but accepted alternative h)	TP

Binary classification with Multi-layer perceptron

In the previous Decision Tree Classifier any of feature scaling techniques was not necessary, because their range does not influence the model. However, for most of the models to perform well standardization or normalization is required. It is recommended to use normalization (Min-Max Scaling) to keep the equal impact of each variable on the predictions, having them in range between 0 and 1 (or -1 and 1). This method is sensitive to outliers. Standardization (Z-score normalization), in turn, uses mean and standard deviation to scale the data. There are no limits for the datapoints, but it assumes to have a Gaussian distribution (in practice sometimes this assumption can be ignored) and transforms the data to have a mean of 0 and a standard deviation of 1. It is worth to notice, that some algorithms require standardization (to provide the centered around zero data) or normalization (to ensure the correct way of learning from the features).

Histograms of the selected columns will help to define the distributions. The values of CO2 equivalent concentration are much higher than values of humidity or temperature. Moreover, we use MLPRegressor (multi-layer perceptron regressor). Thus, normalization is a good choice for this case.

MinMaxScaler from sklearn.preprocessing computes the mean via method fit() and scales the data via transform(). fit_transform() does both steps. Therefore, we implement fit_transform() to the train dataset and use the same computation of mean for the test dataset to avoid any bias.

The same steps are applied for StandardScaler.

x_train, x_test, y_train, y_test = train_test_split(data_1000.loc[:,['Temperature[C]','Humidity[%]','eCO2[ppm]']],data_1000.loc[:,['Fire Alarm']]) # test_size=0.25 

scaler = MinMaxScaler()
x_train=scaler.fit_transform(x_train)
x_test=scaler.transform(x_test)

We repeat the steps of the model creation, fitting and prediction as previously.

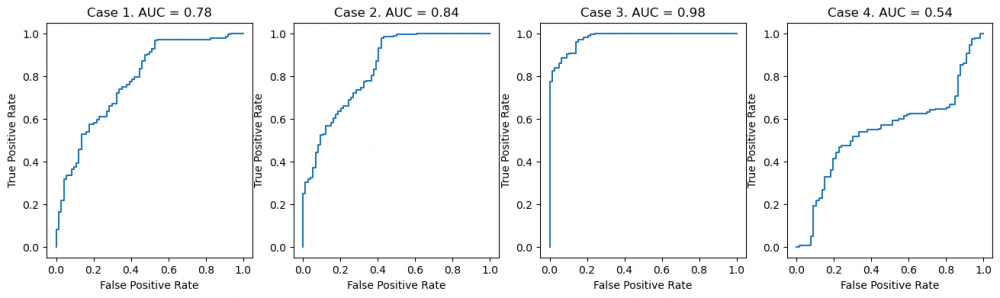
Let us introduce Receiver Operating Characteristic (ROC) and Area Under the curve (AUC). This is a graphical representation of the classification model performance at various thresholds. The threshold can be selected, based on how many FP we are willing to accept. It plots the true positive rate (TPR) versus the false positive rate (FPR) at different classification thresholds.

AUC represents the area under the ROC curve. It measures the overall performance of the binary classification model and has the range between 0 to 1. The greater value, the better model performance. The main goal is to maximize this area in order to have the highest TPR and lowest FPR at the current threshold.

We will create four models in order to do a comparison. Each case has MLPRegressor as a model with different parameters or features from the dataset. By doing this we would like to emphasize the various behaviour of the curve. Then we save the scores, computed for the models, and plot the graphs at the end.

Case I

model_case1 = MLPRegressor(max_iter=100, hidden_layer_sizes = (10,30,10))
model_case1.fit(x_train, y_train)
predictions = model_case1.predict(x_test)

fpr_c1, tpr_c1, _ = metrics.roc_curve(y_test, predictions)
auc_c1 = metrics.roc_auc_score(y_test, predictions)

Case II

model_case2 = MLPRegressor(max_iter=100, hidden_layer_sizes = (60,90,70))
model_case2.fit(x_train, y_train)

predictions = model_case2.predict(x_test)
fpr_c2, tpr_c2, thresholds = metrics.roc_curve(y_test, predictions)
auc_c2 = metrics.roc_auc_score(y_test, predictions)

Case III

x_train, x_test, y_train, y_test = train_test_split(data_1000.loc[:,['Temperature[C]','Humidity[%]','eCO2[ppm]','Raw H2','Raw Ethanol','Pressure[hPa]']],data_1000.loc[:,['Fire Alarm']]) # test_size=0.25 

scaler = MinMaxScaler()
x_train=scaler.fit_transform(x_train)
x_test=scaler.transform(x_test)

model_case3 = MLPRegressor(max_iter=100, hidden_layer_sizes = (10,30,20))
model_case3.fit(x_train, y_train)

predictions = model_case3.predict(x_test)
fpr_c3, tpr_c3, thresholds = metrics.roc_curve(y_test, predictions)
auc_c3 = metrics.roc_auc_score(y_test, predictions)

Case IV

x_train, x_test, y_train, y_test = train_test_split(data_1000.loc[:,['Temperature[C]','Humidity[%]']],data_1000.loc[:,['Fire Alarm']]) # test_size=0.25 

scaler = MinMaxScaler()
x_train=scaler.fit_transform(x_train)
x_test=scaler.transform(x_test)

model_case4 = MLPRegressor(max_iter=10, hidden_layer_sizes = (10,10,10))
model_case4.fit(x_train, y_train)

predictions = model_case4.predict(x_test)
fpr_c4, tpr_c4, thresholds = metrics.roc_curve(y_test, predictions)
auc_c4 = metrics.roc_auc_score(y_test, predictions)

ROC-AUC visualization

fig, ax = plt.subplots(1, 4, figsize=(16, 4))

plt.subplot(141)
plt.plot(fpr_c1,tpr_c1)
plt.subplot(141).set_title("Case 1. AUC = "+str(round(auc_c1,2)))
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')

plt.subplot(142)
plt.plot(fpr_c2,tpr_c2)
plt.subplot(142).set_title("Case 2. AUC = "+str(round(auc_c2,2)))
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')

plt.subplot(143)
plt.plot(fpr_c3,tpr_c3)
plt.subplot(143).set_title("Case 3. AUC = "+str(round(auc_c3,2)))
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')

plt.subplot(144)
plt.plot(fpr_c4,tpr_c4)
plt.subplot(144).set_title("Case 4. AUC = "+str(round(auc_c4,2)))
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')

plt.show()

We can see the improvement of the model from case 1 to case 3. Firstly, we changed the parameter hidden_layer_sizes. Secondly, we selected other features from the dataset. Case 4 stands for the poor performance of the model, where the predictions are close to the random decisions. As you may have assumed AUC closed to 0 means that the model produces opposite outcomes.

Discover other evaluation methods from the module metrics.

1. https://www.emerald.com/insight/content/doi/10.1016/j.aci.2018.08.003/full/pdf

2. https://www.datacamp.com/tutorial/normalization-in-machine-learning

3. https://scikit-learn.org/stable/modules/preprocessing.html#preprocessing-scaler

The author of this entry is Evgeniya Zakharova.