How to Lie with Statistics

THIS ARTICLE IS STILL IN EDITING MODE

Introduction

Statistics, when utilized in a misleading manner, have the potential to deceive the casual observer into believing something contrary to the actual data. Misuse of statistics can occur accidentally in some cases, while in others, it's purposeful and intended to benefit the perpetrator. When combined with the widespread lack of public statistical literacy and the non-statistical nature of human intuition, this issue is significantly amplified.

The focus of this wiki entry is to shed light on the ways statistical charts, figures, and numbers are frequently misused in both media and public discourse. While there exist various other statistical fallacies, paradoxes, and misuses spanning from data collection to data analysis, they are beyond the scope of this article.

Misleading Graphs

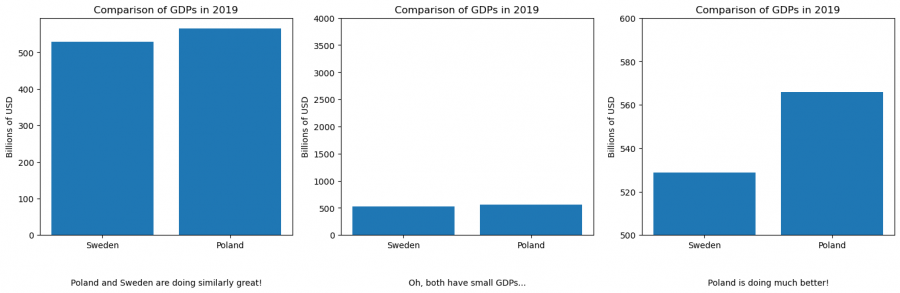
Graphs, despite containing accurate data points, can be presented in misleading ways to emphasize or downplay certain trends. Such misleading graphs can distort reality and are achieved through several techniques: manipulating the y-axis to make differences appear smaller by increasing the shown maximum, making changes seem larger by truncating the bottom of the y-axis, or altering ratios between axes. To counteract these deceptions, axis ratios should remain consistent, ideally starting at 0, or any breaks in the axis should be visually indicated.

import matplotlib.pyplot as plt

values = [528.929, 565.854]
labels = ['Sweden', 'Poland']

statements = ['Poland and Sweden are doing similarly great!', 'Oh, both have small GDPs...', 'Poland is doing much better!']

fig, axs = plt.subplots(1, 3, figsize=(15, 5))

for i, ax in enumerate(axs):
    ax.bar(labels, values)
    ax.set_ylabel('Billions of USD')
    ax.set_title('Comparison of GDPs in 2019')

    ax.text(0.5, -0.2, statements[i], horizontalalignment='center', verticalalignment='top', transform=ax.transAxes)

axs[1].set_ylim(0, 4000)
axs[2].set_ylim(500, 600)

plt.tight_layout()
plt.show()

Another deceptive method involves representing one-dimensional quantities with two- or three-dimensional objects in diagrams. This can occur due to accidental or purposeful misinterpretation of the square-cube law. For instance, if one intends to show that one quantity is double the amount of another and chooses a 3D cube with a doubled side length, the size difference becomes exaggerated because the volume of the cube increases eightfold. Related issues are observed in the use of 3D charts, such as pie or bar charts, presented from specific perspectives, causing identical amounts to occupy differently sized areas in the diagram based on the chosen viewpoint.

One of the trickiest ways to misrepresent statistical data is through map representations. A recent and famous example is the mapping of votes to land areas in the last US president election, resulting in most of the United States being colored red. The deception lies in the fact that states with large rural areas often have sparse populations, yet most of them vote Republican. Consequently, a small number of votes can alter a vast land area, while Democrats tend to concentrate in comparatively smaller urban areas, producing smaller blue dots on the map despite having larger numbers in those spots.

Misinterpreting Statistical Figures

Another issue in statistical result presentation involves confusion regarding percentages. One contributing factor is the frequent lack of distinction between relative percentages, which express change as a ratio in comparison to a specific reference point, and absolute percentages, which represent the same change as a fixed quantity of percentage points in relation to the total. For instance, between 2017 and 2018, the murder rate in New Zealand seemingly surged by an extreme 110%. However, it merely escalated to a value of 1.55 murders per 100,000 citizens, significantly lower than other countries like the US, which reported a rate of 5.3. In reality, New Zealand has one of the lowest murder rates worldwide.

Another factor causing confusion is the shifting base: reducing a value by a certain percentage decreases the base value considered as 100%. Subsequently, if that same value is increased by the same percentage, it calculates to less than the starting value due to the shift in the base.

Statistics are often perceived as more reliable when they yield impressively precise decimal numbers. However, in reality, placing emphasis on error margins better represents the data. Generally, small differences are statistically insignificant and should not be overinterpreted.

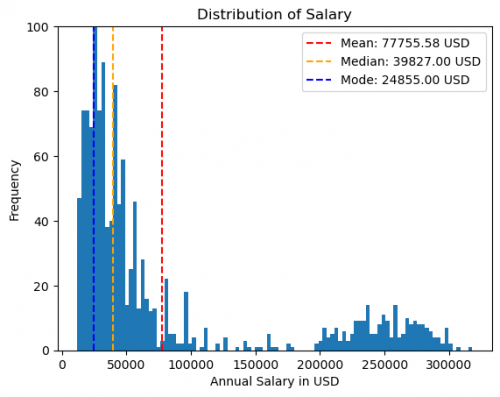
Furthermore, a lack of differentiation between various types of averages leads to misinterpretations. While in most cases where a normal distribution is present, the three averages – mean, median, and mode – tend to be close, so an explicit distinction is not that relevant. In other distributions, they can significantly differ. Consequently, what one perceives as the average might not align with the mean value.

Additionally, percentiles can be misleading as they imply equal distances between different percentile values. However, in most cases, a clustering around the average forms a bell curve, resulting in smaller differences around the middle and larger discrepancies at the extremes.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

df = pd.read_csv("wages.csv")
salary = df['earn']

plt.hist(salary, bins=100)
plt.xlabel('Annual Salary in USD')
plt.ylabel('Frequency')
plt.title('Distribution of Salary')
plt.ylim(0, 100)

mean, median, mode = df['earn'].mean(), df['earn'].median(), df['earn'].mode().values[0]

plt.axvline(mean, color='red', linestyle='--', label=f"Mean: {mean:.2f} USD")
plt.axvline(median, color='orange', linestyle='--', label=f"Median: {median:.2f} USD")
plt.axvline(mode, color='blue', linestyle='--', label=f"Mode: {mode:.2f} USD")

plt.legend()
plt.show()

percentiles = np.percentile(df['earn'], [80, 90, 40, 50])
diff_90_80, diff_50_40 = np.diff(percentiles)[0], np.diff(percentiles)[1]

print("Difference between 90th and 80th percentiles:", diff_90_80)
print("Difference between 50th and 40th percentiles:", diff_50_40)
print("Percentiles encompass different value ranges event though they are both the same 10% apart!")

# Out: Difference between 90th and 80th percentiles 141897.0
# Out: Difference between 50th and 40th percentiles -212463.8
# Out: Percentiles encompass different value ranges event though they are both the same 10% apart!

In this example of salary data, it can be observed that the mean value is earned by only a small fraction of individuals. Most people earn only half as much as indicated by the median. This discrepancy arises from a few high-income earners who significantly skew the mean with their substantial salaries. Depending on your objective, you can portray the salaries as high by utilizing the mean or demonstrate their lower distribution by employing the median and mode...

Conclusions

The described above ways of statistical manipulation to mislead individuals are collectively referred to as “statisticulation”. Depending on chosen representation, statistical information may appear more dramatic or supportive of a particular viewpoint, even if the underlying data remains unchanged.

When confronted with any statistical chart or figure, the recipient must critically and skeptically evaluate it instead of just accepting it at face value. Questioning the motivations and intentions of those presenting the statistic, especially when used to support a specific viewpoint, is vital. An initial warning sign might be when the interpretation contradicts common sense.

According to Hanlon's razor, if a statistic is found to be misleading, it should first be blamed on incompetence before malicious intent is assumed. This piece is intended to raise awareness of how statistics are frequently misrepresented, thereby contributing to the improvement of statistical literacy.

How to Lie with Statistics

Contents

Introduction

Misleading Graphs

Misinterpreting Statistical Figures

Conclusions

Further Reading