Bootstrap Method
In short: The bootstrap method is a resampling technique used to estimate statistics on a population by resampling a dataset with replacement.
Contents
Background
The bootstrap was introduced by Brad Efron in the late 1970s. It is a computer-intensive method for approximating the sampling distribution of any statistic derived from a random sample.
A fundamental problem in statistics is assessing the variability of an estimate derived from sample data.
To test a hypothesis researchers need to sample from population. For each sample results can be different, therefore to estimate population properties researchers need to take many samples. This set of possible study results represents the sampling distribution. With it one can assess the variability in the real-sample estimate (e.g., attach a margin of error to it), and rigorously address questions.
The catch is, that it is costly to repeat studies, and the set of possible estimates is never more than hypothetical. The solution to this dilemma, before the widespread availability of fast computing, was to derive the sampling distribution mathematically. This is easy to do for simple estimates such as the sample proportion, but not so easy for more complicated statistics.
Fast computing helps to resolve the problem and the main method is Efron’s bootstrap.
In practice, the bootstrap is a computerbased technique that uses the core concept of random sampling from a set of numbers and thereby estimates the sampling distribution of virtually any statistic computed from the sample. The only way it differs from the hypothetical resampling is that the repeated samples are not drawn from the population, but rather from the sample itself because the population is not accessible.[1]
What the method does
Bootstrapping is a type of statistical resampling applied to observed data. This method can be used to determine the sampling distribution of a summary statistic (mean, median, and standard deviation) or relationship (correlation and regression coefficient) when these sampling distributions are extremely difficult to obtain analytically.
There are two main ways in which the bootstrap technique can be applied. In the "parametric" method, a knowledge of the data’s distributional form (e.g. Gaussian and exponential) is required. When it is available, such distributional information contributes to greater precision. In the more common "nonparametric" version of bootstrapping, no distributional assumption is needed.
Bootstrap methods are useful when inference is to be based on a complex procedure for which theoretical results are unavailable or not useful for the sample sizes met in practice, where a standard model is suspect, but it is unclear with what to replace it, or where a "quick and dirty" answer is required. They can also be used to verify the usefulness of standard approximations for parametric models, and to improve them if they seem to give inadequate inferences.
Bootstrap resampling
Bootstrapping involves drawing a series of random samples from the original sample with replacement, a large number of times. The statistic or relationship of interest is then calculated for each of the bootstrap samples. The resulting distribution of the calculated values then provides an estimate of the sampling distribution of the statistic or relationship of interest.
Notice that the replacement allows the same value to be included multiple times in the same sample. This is why you can create many different samples.
This is the basic algorithm for resampling with replacement:
- Select an observation from the original sample randomly
- Add this observation to the new sample
- Repeat steps 1 and 2 till the new sample size is equal to the original.
The resulting sample of estimations often leads to a Gaussian distribution. And a confidence interval can be calculated to bound the estimator.
For getting better results, such as that of mean and standard deviation, it is always better to increase the number of repetitions.
Why is the resample of the same size as the original sample?
The variation of the statistic will depend on the size of the sample. If we want to approximate this variation we need to use resamples of the same size.
Bootstrap principle
The bootstrap setup is as follows:
- original sample ( 𝑥1 , 𝑥2 , . . . , 𝑥𝑛 ) is drawn from a distribution 𝐹 .
- 𝑢 is a statistic computed from the sample.
- 𝐹∗ is the empirical distribution of the data (the resampling distribution).
- 𝑥∗1 , 𝑥∗2 , . . . , 𝑥∗𝑛 is a resample of the data of the same size as the original sample.
- 𝑢∗ is the statistic computed from the resample.
Then the bootstrap principle says that:
- 𝐹∗ ≈ 𝐹 .
- The variation of 𝑢 is well-approximated by the variation of 𝑢∗.
Our real interest is in point 2: we can approximate the variation of 𝑢 by that of 𝑢∗ . We will exploit this to estimate the size of confidence intervals. [4]
Bootstrapping for hypothesis testing (using R)
Bootstrapping may be used for constructing hypothesis tests. It is an alternative to statistical inference based on the assumption of a parametric model when that assumption is in doubt, or where parametric inference is impossible or requires complicated formulas for the calculation of standard errors.
R programming language is a strong tool for bootstrap implimintation. There is a special package Boot [5] for bootstrapping. For code transparency, in the examples below we will use base R.
Using R, we will try to reject the null hypothesis that weight of chicks does not differ for casein and meat meal types of feeding.
diet_df <- chickwts #calling standard dataset summary(diet_df) #exploring the data set #Output: # weight feed #Min. :108.0 casein :12 #1st Qu.:204.5 horsebean:10 #Median :258.0 linseed :12 #Mean :261.3 meatmeal :11 #3rd Qu.:323.5 soybean :14 #Max. :423.0 sunflower:12 d <- diet_df[diet_df$feed == 'meatmeal' | diet_df$feed == 'casein',] # choosing "casein" and "meatmeal" for comparison
To understand if two diets actually influence on weight differently we will calculate difference between mean values.
mean_cas <- mean(d$weight[ d$feed == 'casein']) mean_meat <- mean(d$weight[ d$feed == 'meatmeal']) test_stat1 <- abs(mean_cas - mean_meat) round(test_stat1, 2) # Output: # 46.67
For the second estimate we choose difference between medians.
median_cas <- median(d$weight[ d$feed == 'casein']) median_meat <- median(d$weight[ d$feed == 'meatmeal']) test_stat2 <- abs(median_cas - median_meat) round(test_stat2, 2) # Output: # 79
For reference we are going to apply to our dataset three classical approaches to hypothesis testing. To compare two means we use t-test:
t.test(d$weight~d$feed, paired = F, var.eq = F) # H0 - means are equal #Output: # Welch Two Sample t-test # # data: d$weight by d$feed # t = 1.7288, df = 20.799, p-value = 0.09866 # alternative hypothesis: true difference in means is not equal to 0 # 95 percent confidence interval: # -9.504377 102.852861 # sample estimates: # mean in group casein mean in group meatmeal # 323.5833 276.9091
For comparison of medians Wilcoxon rank sum test is suitable:
wilcox.test(d$weight~d$feed, paired = F) # H0 - medians are equal #Output: # Wilcoxon rank sum exact test # # data: d$weight by d$feed # W = 94, p-value = 0.09084 # alternative hypothesis: true location shift is not equal to 0
Kolmagorov-Smirnov test is helpful to understand whether two groups of observations belong to the same distribution:
ks.test(d$weight[d$feed == 'casein'], d$weight[d$feed == 'meatmeal'], pair = F) # H0 - the same distribution #Output: # Two-sample Kolmogorov-Smirnov test # # data: d$weight[d$feed == "casein"] and d$weight[d$feed == "meatmeal"] # D = 0.40909, p-value = 0.1957 # alternative hypothesis: two-sided
Now is the time for bootstrapping. For good performance of resampling the number of samples should be big.
n <- length(d$feed) # the sample size
variable <- d$weight # the variable we will resample from
B <- 10000 # the number of bootstrap samples
set.seed(112358) # for reproducibility
BootstrapSamples <- matrix(sample(variable, size = n*B, replace = TRUE), nrow = n, ncol = B) # generation of samples with replacement
dim(BootstrapSamples) #check dimention of the matrix (23 observations and 10000 samples)
#Output: 2310000
#Initialize the vector to store test statistics
Boot_test_stat1 <- rep(0, B)
Boot_test_stat2 <- rep(0, B)
#Run through a loop, each time calculating the bootstrap test statistics
for (i in 1:B) {
Boot_test_stat1[i] <- abs(mean(BootstrapSamples[1:12,i]) -
mean(BootstrapSamples[13:23,i]))
Boot_test_stat2[i] <- abs(median(BootstrapSamples[1:12,i]) -
median(BootstrapSamples[13:23,i]))
}
#Lets remind ourselves with the observed test statistics values
round(test_stat1, 2)
round(test_stat2, 2)
#Output:
# 46.67
# 79
To understand if the differences between means and medians of two different groups are significant we need to prove that it's highly unlikely that this result is obtained by chance. Here we need a help of p-value.
p-value = the number of bootstrap test statistics that are greater than the observed test statistics/ B(the total number of bootstrap test statistics)
Lets find p-value for our hypothesis.
p_value_means <- mean(Boot_test_stat1 >= test_stat1) p_value_means #Output: #0.0922
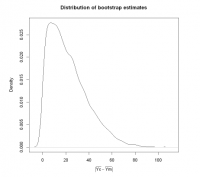
Interpretation: Out of the 10000 bootstrap test statistics calculated, 922 of them had test statistics greater than the observed one. If there is no difference in the mean weights, we would see a test statistic of 46.67 or more by chance roughly 9% of the time
p_value_medians <- mean(Boot_test_stat2 >= test_stat2) p_value_medians # Output: # 0.069
690 of bootstrap median differences are greater or equal than observed one.
Conclusion
Therefore, classical and bootsrapping hypothesis tests gave close results, that there is no statistically significant difference in weight of chicks with two diets (casein and meatmeal). However p-values are pretty low even with such little sample size. Even if we failed to reject the null hypothesis, we need to test it again with bigger sample size.
plot(density(Boot_test_stat1), xlab = expression(group('|', bar(Yc) - bar(Ym), '|')), main = 'Distribution of bootstrap estimates')
Bootstrapping for confidence interval (using R)
An important task of statistics is to establish the degree of trust that can be placed in a result based on a limited sample of data.[4]
We are going to apply bootstrapping to build the confidence interval. Using R, we will build the confidence interval for the difference between weight of chicks with casein and meatmeal types of feeding. Main estimates will be differences in means and medians.
Diff_In_Means <- mean_cas - mean_meat round(Diff_In_Means, 2) #Output: 46.67 Diff_In_Medians <- (median_cas - median_meat ) #diff in medians round(Diff_In_Medians, 2) #Output: 79
Now we are going to generate bootstrap samples separately for casein sample and meatmeal sample.
set.seed(13579) # set a seed for consistency/reproducability
n.c <- 12 # the number of observations to sample from casein
n.m <- 11 # the number of observations to sample from meatmeal
B <- 100000 # the number of bootstrap samples
# now, get those bootstrap samples (without loops!)
# stick each Boot-sample in a column...
Boot_casein <- matrix(sample(d$weight[d$feed=="casein"], size= B*n.c,
replace=TRUE), ncol=B, nrow=n.c)
Boot_meatmeal <- matrix(sample(d$weight[d$feed=="meatmeal"], size= B*n.m,
replace=TRUE), ncol=B, nrow=n.m)
Let's check the distributions of bootstrap sample means.
Boot_test_mean_1 <- apply(Boot_casein, MARGIN = 2, mean)
Boot_test_mean_2 <- apply(Boot_meatmeal, MARGIN = 2, mean)
b <- min(c(Boot_test_mean_1, Boot_test_mean_2))# - 0.001 # Set the minimum for the breakpoints
e <- max(c(Boot_test_mean_1, Boot_test_mean_2)) # Set the maximum for the breakpoints
ax <- pretty(b:e, n = 110) # Make a neat vector for the breakpoints
hist1 <- hist(Boot_test_mean_1, breaks = ax, plot = FALSE)
hist2 <- hist(Boot_test_mean_2, breaks = ax, plot = FALSE)
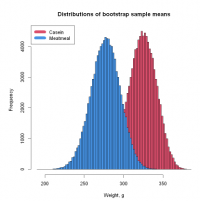
print(paste('Mean weight casein', round(mean_cas, 1)))
print(paste('Mean weight meatmeal', round(mean_meat, 1)))
plot(hist1, col = 2, xlab = 'Weight, g', main = 'Distributions of bootstrap sample means') # Plot 1st histogram using a transparent color
plot(hist2, col = 4, add = TRUE) # Add 2nd histogram using different color
legend("topleft", c('Casein', 'Meatmeal'), col = c(2, 4), lwd = 10)
# Output:
# [1] "Mean weight casein 323.6"
# [1] "Mean weight meatmeal 276.9"
We can see that bootstrap sample means are normally distributed. Mean of the bootstrap distribution is equal to the mean of original sample.
# check dimentions of matrices(100000 samples, 12 and 11 observations for casein and meatmeal respectively) dim(Boot_casein) dim(Boot_meatmeal) # Output: # 12 * 100000 # 11 * 100000
Next step is calculating differences in means and medians among bootstrap samples of casein and meatmeal.
# calculate the difference in means for each of the bootsamples Boot_Diff_In_Means <- colMeans(Boot_casein) - colMeans(Boot_meatmeal) # look at the first 10 differences in means round(Boot_Diff_In_Means[1:10], 1) # Output: # 49.5* 48.6* 32.2* 68.6* 46.2* 65.5* 72.2* 29.9* 10.1* 50.1 # calculate the difference in medians for each of the bootsamples Boot_Diff_In_Medians <- apply(Boot_casein, MARGIN=2, FUN=median) - apply(Boot_meatmeal, MARGIN=2, FUN=median) # and, look at the first 10 diff in medians Boot_Diff_In_Medians[1:10] # Output: # 27* 39* 0* 87.5* 62* 96* 67* 42.5* 3* 72
Common approaches to building a bootstrap confidence interval:
- Percentile method
- Basic method
- Normal method
- Bias-Corrected method.
We will choose the first one as the most intuitive. Percentile method takes the entire set of bootstrap estimates and in order to form a 95 % confidence interval the 2.5th percentile of all the bootstrap estimates or bootstrap distribution used as the lower bound for the interval and 97.5th percentile - as upper bound.
# first, for the difference in MEANS quantile(Boot_Diff_In_Means, prob=0.025) quantile(Boot_Diff_In_Means, prob=0.975) # Output: # 2.5%: -3.73503787878789 # 97.5%: 97.0079545454545
We are 95 % confident that the mean weight for casein diet is between 3.73 g lower up to 97.01 g higher than for meatmeal diet.
# and then, the difference in MEDIANS quantile(Boot_Diff_In_Medians, prob=0.025) quantile(Boot_Diff_In_Medians, prob=0.975) # Output: # 2.5%: -22 # 97.5%: 116
We are 95 % confident that the median weight for casein diet is between 22 g lower up to 116 g higher than for meatmeal diet.
Conclusion
We can see that both intervals contain 0. From this we can deduce that differences of the means or the medians are not statistically significant.
Strengths & Challenges
Strengths of bootstrapping
- Good for checking parametric assumptions.
- Avoids the costs of taking new samples (estimate a sampling distribution when only one sample is available).
- Used when parametric assumptions can not be made or are very complicated.
- Does not require large sample size.
- Simple method to estimate parameters and standard errors when adequate statistical theory is unavailable.
- Useful to check stability of results.
- Works for different statistics — for example, a mean, median, standard deviation, proportion, regression coefficients and Kendall’s correlation coefficient.
- Helps to indirectly assess the properties of the distribution underlying the sample data.
Challenges
- Even if bootstrapping is asymptotically consistent, it does not provide general finite-sample guarantees.
- The result may depend on the representative sample.
- The apparent simplicity may conceal the fact that important assumptions are being made when undertaking the bootstrap analysis (e.g. independence of samples).
- Bootstrapping can be time-consuming.
- There is a limitation of information that can be obtained through resampling even if number of bootstrap samples is large.
Normativity
Bootstrap methods offer considerable potential for modelling in complex problems, not least because they enable the choice of estimator to be separated from the assumptions under which its properties are to be assessed.
Although the bootstrap is sometimes treated as a replacement for "traditional statistics". But the bootstrap rests on "traditional" ideas, even if their implementation via simulation is not "traditional".
The computation can not replace thought about central issues such as the structure of a problem, the type of answer required, the sampling design and data quality.
Moreover, as with any simulation experiment, it is essential to monitor the output to ensure that no unanticipated complications have arisen and to check that the results make sense. The aim of computing is insight, not numbers.[2]
Outlook
Over the years bootstrap method has seen a tremendous improvement in its accuracy level. Specifically improved computational powers have allowed for larger possible sample sizes used for estimation. As bootstrapping allows to have much better results with less amount of data, the interest for this method rises substantially in research field. Furthermore, bootstrapping is applied in machine learning to assess and improve models. In the age of computers and data driven solutions bootstrapping has good perspectives for spreading and development.
Key Publications
- Efron, B. (1982) The Jackknife, the Bootstrap, and Other Resampling Plans. Philadelphia: Society for Industrial and Applied Mathematics.
- Efron, B. and Tibshirani, R. J. (1993) An Introduction to the Bootstrap. New York: Chapman and Hall.
References
- Dennis Boos and Leonard Stefanski. Significance Magazine, December 2010. Efron's Bootstrap.
- A. C. Davison and Diego Kuonen. Statistical Computing & Statistical Graphics Newsletter. Vol.13 No.1. An Introduction to the Bootstrap with Applications in R
- Michael Wood. Significance, December 2004. Statistical inference using bootstrap confidence interval.
- Jeremy Orloff and Jonathan Bloom. Bootstrap confidence intervals. Class 24, 18.05.
- CRAN documentation. Package "bootstrap", June 17, 2019.
Further Information
Youtube video. Statquest. Bootstrapping main ideas
Youtube video. MarinStatsLectures. Bootstrap Confidence Interval with R
Youtube video. MarinStatsLectures. Bootstrap Hypothesis Testing in Statistics with Example
Article. A Gentle Introduction to the Bootstrap Method
Article. Jim Frost. Introduction to Bootstrapping in Statistics with an Example
The author of this entry is Andrei Perov.