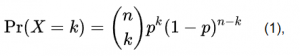Binomial distribution
THIS ARTICLE IS STILL IN EDITING MODE
Contents
Definition
Binomial distribution is a probability distribution that summarises the likelihood that a variable will take one of two independent values under a given set of parameters. The distribution is obtained by performing a number of Bernoulli trials. Each trial is completely independent of all others.
A Bernoulli trial is assumed to meet each of these criteria:
- there must be only 2 possible outcomes;
- each outcome has a fixed probability of occurring. A success has the probability of p, and a failure has the probability of 1 – p.
Binomial Distribution is a discrete distribution, whcih describes the outcome of binary scenerios. Discrete distribution is defined at separate set of events, e.g., a coin toss's result is discrete as it can be only head or tail, while the people`s height is continuous, as it can be 170, 170.01, 170.11 and so on. Binomial distribution will be quite similar to normal distribution with certain loc and scale, if there are enough data points.
Binomial Distribution Formula
There is a Binomial distribution formula. With its help we can calculate the probability, that the event will occur k times in n number of trails.
where p - a probability of success, 1 – p - a probability of failure, n - number of trails, k - number of successes and
![]()
Example
Consider a random experiment of tossing a biased coin 6 times, where the probability of getting a head is 0.6. If "getting a head" is considered as "success" then, the binomial distribution table will contain the probability of r successes P(r) for each possible value of r. By substituting into the formula (1) (p=0.6, 1-p=0.4, n=6, k=(0,1,2,3,4,5,6)), we will get the following table of the binomial distribution:
| r | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P(r) | 0.004096 | 0.036864 | 0.138240 | 0.276480 | 0.311040 | 0.186624 | 0.046656 |
Binomial distribution in Python
Now, we will use Python to analyse the distribution and plot the graph.
from numpy import random x = random.binomial(n=21, p=0.5, size=21) print(x)
[10 7 10 11 8 10 12 14 11 7 8 6 8 12 14 8 11 14 16 11 10]
random.binomial has three parameters:
- n - number of trails;
- p - probability of occurance of each trial;
- size - the shape of the returned array.
It returns the array with number of success in n=21 trials. More information about this functions can be found here.
Visualization
import matplotlib.pyplot as plt import seaborn as sns sns.displot(random.binomial(n=10, p=0.5, size=100)) plt.show() # Figure 1
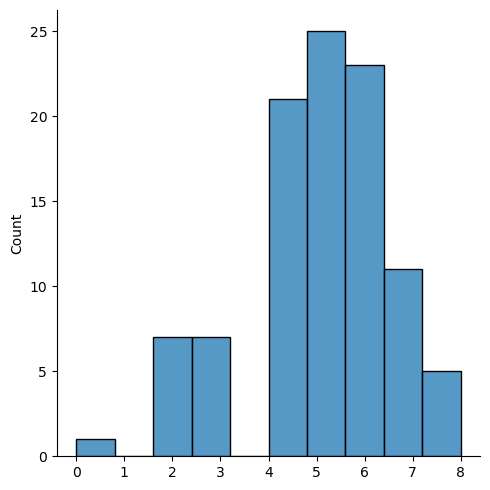
Figure 1: Binomial distribution plot
Python Calculation: Coin Flip Prediction
Using the math Library
We can implement the binomial distribution of getting an even number of heads in 21 flips of unbiased coins using the math library in Python. For each value of i in the range 0 to 22 (exclusive), with a step of 2, we can calculate the corresponding probability of getting i heads using the binomial distribution formula.
Inside the loop, we can first calculate the number of ways to choose i heads out of 21 flips using the math.comb() function. We can then calculate the probability of getting exactly i heads in 21 flips, which is (1/2)21. Finally, we can multiply the two values to obtain the probability of getting exactly i heads in 21 flips and store it in a list called probabilities.
After the loop finishes, we can compute the sum of all the probabilities, stored in the list probabilities using the sum() function and print the total probability of getting an even number of heads in 21 flips.
import math
# Create an empty list to store the probabilities of getting an even number of heads
probabilities = []
# Loop over all even numbers of heads that can be obtained in 21 flips
for i in range(0, 22, 2):
# Calculate the number of ways to choose i heads out of 21 flips
m = math.comb(21, i)
# Calculate the probability of getting i heads in 21 flips
n = (1/2 ** 21)
prob = m * n
# Append the probability to the list
probabilities.append(prob)
# Loop over the probabilities and print the probability of getting each even number of heads
for i, prob in enumerate(probabilities):
print("The probability of getting {} heads in 21 flips is {}.".format(2*i, prob))
# Calculate the total probability
total_prob = sum(probabilities)
print("Total probability of getting even number of heads is {}".format(total_prob))
The probability of getting 0 heads in 21 flips is 4.76837158203125e-07.
...
The probability of getting 10 heads in 21 flips is 0.16818809509277344.
...
Total probability of getting even number of heads is 0.5
Using the SciPy Library
This time, we will use the pre-built function to calculate the probability.
1. Import the binom() function from the scipy.stats module.
2. Define the binomial distribution with n trials and probability p of success using the binom() function.
We calculate the probability of getting an even number of heads (0, 2, 4, …, 20) using the pmf() method of the binomial distribution.
It returns the probability mass function (PMF) of the distribution for each value in the given range.
Then we implement another for-loop to print the probability of getting each even number of heads in the list even_probs.
Finally, we calculate the total probability of getting an even number of heads in 21 flips by summing up the probabilities in the list even_probs.
from scipy.stats import binom
n = 21
p = 0.5
# Define the binomial distribution with n trials and probability p of success
binom_dist = binom(n, p)
# Calculate the probability of getting an even number of heads (0, 2, 4, ..., 20)
even_probs = binom_dist.pmf(range(0, 22, 2))
# Print the probability of getting each even number of heads
for i, prob in enumerate(even_probs):
print("The probability of getting {} heads in 21 flips is {}".format(2*i,prob))
# Calculate the total
total_prob = sum(even_probs)
print("Total probability of getting even number of heads is {}".format(total_prob))
The probability of getting 0 heads in 21 flips is 4.768371582031256e-07
...
The probability of getting 10 heads in 21 flips is 0.16818809509277355
...
Total probability of getting even number of heads is 0.5000000000000002
Scipy library provides a more efficient and convenient calculation method. It allows us to define and calculate the distribution in just a few lines of code.
Why are the Results (Slightly) Different?
The difference between the SciPy and math calculations is due to floating-point precision errors. In computer programming, floating-point numbers are represented in a limited number of bits, which can cause a loss of precision when performing calculations. This is why we are getting slightly different values for the probabilities of getting an even number of heads when comparing the results of the two methods.
Both methods provide a good approximation of the true probability, and the difference between the two is negligible for most practical purposes.
The author of this entry is Raj Chaudhari. Edited by Evgeniya Zakharova.